题目内容
17.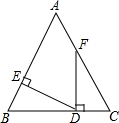 如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )| A. | 160° | B. | 150° | C. | 140° | D. | 120° |
分析 由DF⊥BC有∠FDB=90°,而∠EDF=70°,根据三角形内角和定理得到∠BDE=90°-70°=20°,由DE⊥AB得到∠DEB=90°,根据三角形内角和定理得到求出∠B的度数和∠C的度数,进而求出∠CFD的度数,利用邻补角的知识求出∠AFD的度数.
解答 解:∵DF⊥BC,
∴∠FDB=90°,
而∠EDF=70°,
∴∠BDE=90°-70°=20°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠B=180°-∠DEB-∠BDE=180°-90°-20°=70°,
∴∠C=∠B=70°,
∴∠CFD=90°-70°=20°,
∴∠AFD=180°-20°=160°.
故选A.
点评 本题主要考查了等腰三角形的性质以及三角形内角和的知识,解题的关键是求出∠B和∠C的度数,此题难度不大.

练习册系列答案
相关题目
5.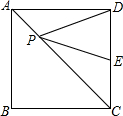 如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
 如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )| A. | 3$\sqrt{10}$ | B. | 10$\sqrt{3}$ | C. | 9 | D. | 9$\sqrt{2}$ |
12.关于x的方程ax2-2x+1=0有两个实数根,则a的取值范围是( )
| A. | .a≤1 | B. | .a<1 | C. | .a≤1且a≠0 | D. | a<1且a≠0 |
7. 如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )
如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )
 如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )
如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )| A. | 5 cm | B. | 6 cm | C. | 7 cm | D. | 8 cm |
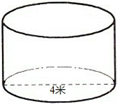 有一个圆柱形的蓄水池底面直径为4米,深为2.5米.
有一个圆柱形的蓄水池底面直径为4米,深为2.5米.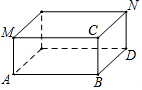 如图,有一个长方体无盖的盒子,长AB=8cm,宽BD=5cm,高BC=1cm,一只蚂蚁经过盒子里面从N爬到M.
如图,有一个长方体无盖的盒子,长AB=8cm,宽BD=5cm,高BC=1cm,一只蚂蚁经过盒子里面从N爬到M.