题目内容
12．在各个内角都相等的多边形中，一个内角是一个外角的4倍，则这个多边形是几边形？这个多边形的内角和是多少度？分析 首先设多边形的边数为n，根据多边形内角和公式180°（n-2）和多边形外角和为360°，可得方程180（n-2）=360×4，再解即可得边数，再利用内角和公式即可得到结论．
解答 解：设多边形的边数为n，
180（n-2）=360×4，
解得：n=10，
这个多边形的内角和=（10-2）×180=1440（度）．
答：这个多边形是10边形，这个多边形的内角和是1440度．
点评 此题主要考查了多边形的内角和外角，关键是掌握多边形内角和公式180°（n-2），多边形外角和为360°．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
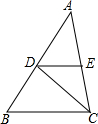如图，CD平分∠ACB，DE∥BC，∠AED=76°，求∠EDC的度数．
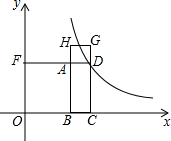已知点D是反比例函数上一点，矩形ABCD的周长是16，正方形ABOF和正方形ADGH的面积之和为50，则反比例函数的解析式是$y=\frac{8}{x}$或$y=\frac{56}{x}$．