题目内容
2．
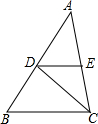如图，CD平分∠ACB，DE∥BC，∠AED=76°，求∠EDC的度数．
分析 根据平行线的性质求得∠ACB的度数，然后根据角平分线的定义求得∠DCB的度数，然后利用两直线平行，内错角相等即可求解．
解答 解：∵DE∥BC，
∴∠ACB=∠AED=76°，
又∵CD的平分∠ACB，
∴∠DCB=$\frac{1}{2}$∠ACB=38°，
∵DE∥BC，
∴∠EDC=∠DCB=38°．
点评 本题考查了平行线的性质、角平分线的定义以及三角形的内角和定理，解答本题的关键是掌握两直线平行，同位角相等以及两直线平行，内错角相等，此题是基础知识要熟练掌握．
练习册系列答案
相关题目
13．下列各式中，是关于x，y的二元一次方程的是（ ）
| A． | 2x-y | B． | x-3y=-15 | C． | xy+x-2=0 | D． | $\frac{2}{x}$-y=0 |
10．
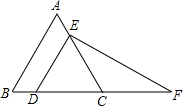如图，在等边三角形ABC中，点D，E分别在边BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F；若△CEF一边的长为2，则△CEF的周长为（ ）
如图，在等边三角形ABC中，点D，E分别在边BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F；若△CEF一边的长为2，则△CEF的周长为（ ）| A． | 4+2$\sqrt{3}$ | B． | 4+2$\sqrt{3}$或2+$\frac{4}{3}$$\sqrt{3}$ | C． | 2+2$\sqrt{3}$或2+$\frac{4}{3}$$\sqrt{3}$ | D． | 4+2$\sqrt{3}$或2+$\frac{2}{3}$$\sqrt{3}$ |
7．下列运算正确的是（ ）
| A． | a2+a3=a5 | B． | （-a3）2=a6 | C． | 3a2•2a3=6a6 | D． | （a-b）2=a2-b2 |