题目内容
20.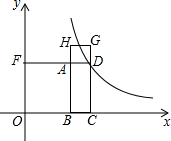 已知点D是反比例函数上一点,矩形ABCD的周长是16,正方形ABOF和正方形ADGH的面积之和为50,则反比例函数的解析式是$y=\frac{8}{x}$或$y=\frac{56}{x}$.
已知点D是反比例函数上一点,矩形ABCD的周长是16,正方形ABOF和正方形ADGH的面积之和为50,则反比例函数的解析式是$y=\frac{8}{x}$或$y=\frac{56}{x}$.
分析 设点D坐标为(x,y),根据矩形ABCD的周长是16、正方形ABOF和正方形ADGH的面积之和为50可得(x-y)2+y2=50、(x-y)+y=8,可求得x、y的值,继而可得函数解析式.
解答 解:设D点坐标为(x,y),
则正方形ABOF的边长为y,正方形ADGH的边长为x-y,BC=OC-OB=x-y,
根据题意得(x-y)2+y2=50,(x-y)+y=8,
解得:x=8,y=1或y=7,
则xy=8或xy=56,
∴反比例函数的解析式为$y=\frac{8}{x}$或$y=\frac{56}{x}$.
故答案为:$y=\frac{8}{x}$或$y=\frac{56}{x}$.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
10.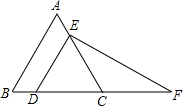 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )
 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )| A. | 4+2$\sqrt{3}$ | B. | 4+2$\sqrt{3}$或2+$\frac{4}{3}$$\sqrt{3}$ | C. | 2+2$\sqrt{3}$或2+$\frac{4}{3}$$\sqrt{3}$ | D. | 4+2$\sqrt{3}$或2+$\frac{2}{3}$$\sqrt{3}$ |
10.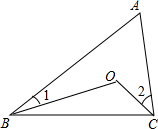 如图,点O是△ABC内一点,∠A=80°∠1=15°,∠2=40°,则∠BOC的度数为( )
如图,点O是△ABC内一点,∠A=80°∠1=15°,∠2=40°,则∠BOC的度数为( )
 如图,点O是△ABC内一点,∠A=80°∠1=15°,∠2=40°,则∠BOC的度数为( )
如图,点O是△ABC内一点,∠A=80°∠1=15°,∠2=40°,则∠BOC的度数为( )| A. | 45° | B. | 55° | C. | 135° | D. | 150° |