题目内容
1.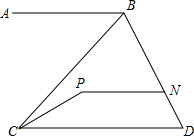 如图,已知AB∥PN∥CD.
如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;
(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.
分析 (1)由平行线的性质得出∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,即可得出结论;
(2)由(1)的结论代入计算即可.
解答 解:(1)∠ABC-∠BCP+∠CPN=180°;理由如下:
延长NP交BC于M,如图所示:
∵AB∥PN∥CD,
∴∠ABC=∠BMN=∠BCD,∠CPN+∠PCD=180°,
∵∠PCD=∠BCD-∠BCP=∠ABC-∠BCP,
∴∠ABC-∠BCP+∠CPN=180°.
(2)由(1)得:∠ABC-∠BCP+∠CPN=180°,
则∠BCP=∠ABC+∠CPN-180°=155°+42°-180°=17°.
点评 本题考查了平行线的性质;熟记平行线的性质是解决问题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
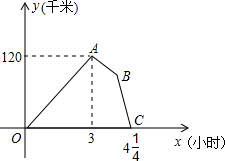 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后,卸完物品再另装货物共用45min,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后,卸完物品再另装货物共用45min,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示. 如图,一个圆柱体和一个长方体组成的几何体,则其主视图是( )
如图,一个圆柱体和一个长方体组成的几何体,则其主视图是( )



 如图,AB∥DC,AD∥BC,E为BC延长线上一点,连结AE与CD相交于点F,若∠CFE=∠E. 试说明AE平分∠BAD.
如图,AB∥DC,AD∥BC,E为BC延长线上一点,连结AE与CD相交于点F,若∠CFE=∠E. 试说明AE平分∠BAD. 如图,已知AB∥CD,AC平分∠DAB,且∠DCA=28°,∠B=96°.
如图,已知AB∥CD,AC平分∠DAB,且∠DCA=28°,∠B=96°. 如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O.求证:OE=OF.
如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O.求证:OE=OF.