题目内容
10. 如图,已知AB∥CD,AC平分∠DAB,且∠DCA=28°,∠B=96°.
如图,已知AB∥CD,AC平分∠DAB,且∠DCA=28°,∠B=96°.(1)求∠DCE的度数;
(2)求∠D的度数.
分析 (1)由平行线的性质得出同位角相等即可;
(2)由平行线的性质得出∠BAC=∠DCA=28°,由角平分线得出∠DAB=2∠BAC=56°,再由平行线的性质得出同旁内角互补,即可得出结果.
解答 解:(1)∵AB∥CD,
∴∠DCE=∠B=96°;
(2)∵AB∥CD,
∴∠BAC=∠DCA=28°,
∵AC平分∠DAB,
∴∠DAB=2∠BAC=56°,
∵AB∥CD,
∴∠D+∠BAD=180°,
∴∠D=180°-56°=124°.
点评 本题考查了平行线的性质、角平分线的定义;熟记平行线的性质是解决问题的关键.

练习册系列答案
相关题目
5. 如图,直线AB∥CD,EF⊥CE,垂足为E,EF交CD于点F,∠1=48°,则∠2的度数是( )
如图,直线AB∥CD,EF⊥CE,垂足为E,EF交CD于点F,∠1=48°,则∠2的度数是( )
 如图,直线AB∥CD,EF⊥CE,垂足为E,EF交CD于点F,∠1=48°,则∠2的度数是( )
如图,直线AB∥CD,EF⊥CE,垂足为E,EF交CD于点F,∠1=48°,则∠2的度数是( )| A. | 42° | B. | 48° | C. | 52° | D. | 58° |
20.计算(-3a-bc)•(bc-3a)的结果等于( )
| A. | bc2-9a2 | B. | b2c2-3a2 | C. | 9a2-b2c2 | D. | b2c2-9a2 |
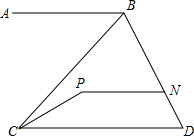 如图,已知AB∥PN∥CD.
如图,已知AB∥PN∥CD.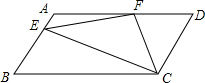 如图所示,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段上,连接EF、CF,则下列结论
如图所示,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段上,连接EF、CF,则下列结论