题目内容
11. 如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O.求证:OE=OF.
如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O.求证:OE=OF.
分析 先依据HL证明Rt△ABE≌Rt△CDF,由全等三角形的性质可知AE=CF,然后证明AE∥CF,故此可证明四边形AECF为平行四边形,最后依据平行四边形的性质证明即可.
解答 证明:在Rt△ABE和Rt△CDF中,
$\left\{\begin{array}{l}{AB=CD}\\{BE=DF}\end{array}\right.$,
∴Rt△ABE≌Rt△CDF.
∴AE=CF.
又∵AE⊥BD,CF⊥BD,
∴AE∥CF.
∴四边形AECF为平行四边形.
∴OE=OF.
点评 本题主要考查的是全等三角形的性质和判定、平行四边形的性质和判定,证得四边形AECF为平行四边形是解题的关键.

练习册系列答案
相关题目
6. 下面几何体的左视图是( )
下面几何体的左视图是( )
 下面几何体的左视图是( )
下面几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
3.已知m,n是方程x2-2x-1=0的两根,且(2m2-4m+a)(3n2-6n-7)=8,则a的值等于( )
| A. | -4 | B. | -2 | C. | 4 | D. | 2 |
20.计算(-3a-bc)•(bc-3a)的结果等于( )
| A. | bc2-9a2 | B. | b2c2-3a2 | C. | 9a2-b2c2 | D. | b2c2-9a2 |
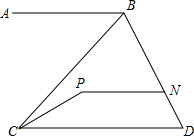 如图,已知AB∥PN∥CD.
如图,已知AB∥PN∥CD.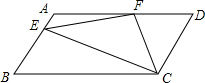 如图所示,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段上,连接EF、CF,则下列结论
如图所示,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段上,连接EF、CF,则下列结论 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )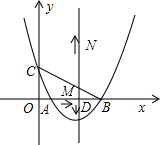 △ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.
△ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.