题目内容
19. 如图,△ABC中,AC=6,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则线段OC长为7$\sqrt{2}$.
如图,△ABC中,AC=6,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则线段OC长为7$\sqrt{2}$.
分析 过点O作OM垂直于CA于点N,作ON垂直于CB于点N,易证四边形MCNO是矩形,利用已知条件再证明△AOM≌△BON,因为OM=ON,所以AM=BN,进而求出CN的长,根据勾股定理即可求出OC的长.
解答 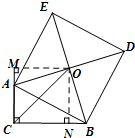 解:过点O作OM垂直于CA于点N,作ON垂直于CB于点N,
解:过点O作OM垂直于CA于点N,作ON垂直于CB于点N,
∴∠OMC=∠ONC=90°,
∵∠ACB=90°,
∴四边形MCNO是矩形,
∴∠MON=90°,
∵正方形 ABDE对角线交于点O,
∴OA=OB,∠AOB=90°,
∴∠MON-∠AON=∠AOB-∠AON,
∴∠AOM=∠NOB,
∵∠OMA=∠ONB=90°,
在△AOM和△BON中,
$\left\{\begin{array}{l}{∠AOM=∠BON}\\{∠OMA=∠ONB=90°}\\{OA=OB}\end{array}\right.$,
∴△AOM≌△BON(AAS),
∴OM=ON,
∴AM=BN,
∵AC=6,BC=8,
∴CN=$\frac{AC+BC}{2}$=7,
∵∠OCN=45°,
∴ON=CN=7,
由勾股定理得OC=7$\sqrt{2}$,
故答案为7$\sqrt{2}$.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
11.下列各式“-(-2),-|-2|,-22,-(-2)2计算结果为负数的个数有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
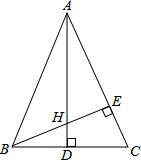 已知在△ABC中,∠BAC是锐角,AB=AC,AD和BE是高,且AE=BE,求证:AH=2BD.
已知在△ABC中,∠BAC是锐角,AB=AC,AD和BE是高,且AE=BE,求证:AH=2BD. 如图,在△ABC中,AC=BC=5,AB=8,过点C作CG⊥AB,垂足为点G,以AC为边向外作△ACD,且AC=DC,∠ACD=50°,点E在边AB上,以E为顶点作∠CEA=50°,点E在边AB上,以E为顶点作∠CEA=50°,过点D作DF⊥CE,交EC的延长线于点F.
如图,在△ABC中,AC=BC=5,AB=8,过点C作CG⊥AB,垂足为点G,以AC为边向外作△ACD,且AC=DC,∠ACD=50°,点E在边AB上,以E为顶点作∠CEA=50°,点E在边AB上,以E为顶点作∠CEA=50°,过点D作DF⊥CE,交EC的延长线于点F.