题目内容
3.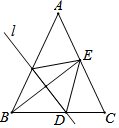 如图,在△ABC中,AB=AC=12$\sqrt{5}$,BC=24,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.
如图,在△ABC中,AB=AC=12$\sqrt{5}$,BC=24,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.
分析 利用三线合一得到G为BC的中点,求出GC的长,过点A作AG⊥BC于点G,在直角三角形AGC中,根据勾股定理求出AG的长,再由E为AC中点,可得EF、FC的长,在直角三角形DEF中,利用勾股定理求出x的值,即可确定出BD的长.
解答 解:过点A作AG⊥BC于点G,
∵AB=AC=12$\sqrt{5}$,BC=24,
∴GC=BG=12,
∴AG=24,
∵将△ABC沿直线l翻折后,点B落在边AC的中点处,
过E点作EF⊥BC于点F,
∴EF=$\frac{1}{2}$AG=12,
∴FC=$\frac{1}{2}$GC=6,
设BD=x,则DE=x,
∴DF=24-x-6=18-x,
∴x2=(18-x)2+122,
解得:x=13,
则BD=13.
故答案为:13.
点评 此题主要考查了翻折变换的性质以及勾股定理、相似三角形的性质等,根据已知表示出DE的长是解题关键.

练习册系列答案
相关题目
13.荆楚网消息,10月7日,武汉铁路局“十一”黄金周运输收官,累计发送旅客640万人,640万用科学记数法表示为( )
| A. | 6.4×102 | B. | 640×104 | C. | 6.4×106 | D. | 6.4×105 |
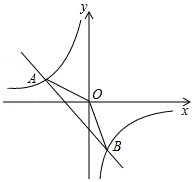 如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.
如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.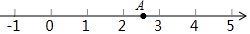 如图所示的数轴上,
如图所示的数轴上,