题目内容
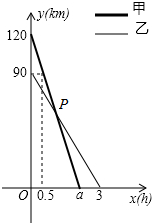 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图,请回答下列问题:
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图,请回答下列问题:(1)A、C两村间的距离为
(2)分别求出y1,y2行驶时间x(h)之间的函数关系式?
(3)求出图中点P的坐标,并解释该点坐标所表示的实际意义;
(4)乙在行驶过程中,请直接写出当x=
考点:一次函数的应用
专题:图表型
分析:(1)根据图象得到甲的运动速度即可解决问题;
(2)首先求出乙的运动速度,结合图象即可解决问题;
(3)由题意及图象可知,在点P处甲乙二人相遇,问题即可解决;
(4)根据题意结合图形即可解决问题.
(2)首先求出乙的运动速度,结合图象即可解决问题;
(3)由题意及图象可知,在点P处甲乙二人相遇,问题即可解决;
(4)根据题意结合图形即可解决问题.
解答: 解:(1)由图象可知:
解:(1)由图象可知:
甲运动0.5小时共行驶30km,
∴甲运动的速度为每小时60km,
∵A、C两村间的距离为120km,
∴甲从A村到C村共用时间a=2h,
故该题答案为120,2.
(2)由题意知:
乙从B村到C村行驶了90km,共用时间3h,
∴行驶速度为每小时30km,
∴y1=-60t+120,y2=-30t+90.
(3)当y1=y2时,
-60t+120=-30t+90,
解得:t=1,
∴甲乙二人行驶1小时后两人相遇,
此时距离C村60km,
故P点坐标为P(1,60).
(4)乙在行驶过程中,当x=
,
,
(h)时距甲10km.
 解:(1)由图象可知:
解:(1)由图象可知:甲运动0.5小时共行驶30km,
∴甲运动的速度为每小时60km,
∵A、C两村间的距离为120km,
∴甲从A村到C村共用时间a=2h,
故该题答案为120,2.
(2)由题意知:
乙从B村到C村行驶了90km,共用时间3h,
∴行驶速度为每小时30km,
∴y1=-60t+120,y2=-30t+90.
(3)当y1=y2时,
-60t+120=-30t+90,
解得:t=1,
∴甲乙二人行驶1小时后两人相遇,
此时距离C村60km,
故P点坐标为P(1,60).
(4)乙在行驶过程中,当x=
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
点评:该命题主要考查了一次函数的图象及其应用问题;解题的关键是准确找出图象中隐含的数量信息,灵活利用函数图象来分析、判断、推理或解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
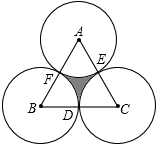 如图,正△ABC的边长为a,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,
如图,正△ABC的边长为a,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,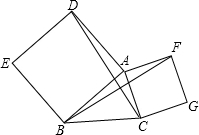 以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.
以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.