题目内容
某商店销售一种商品,通过记录,发现该商品从开始销售至销售的第x天结束时(x为整数)的总销量y(件)满足二次函数关系,销量情况记录如下表:
(1)求y与x之间的函数关系式(不需要写自变量的取值范围);
(2)求:销售到第几天结束时,该商品全部售完?
(3)若第m天的销量为22件,求m的值.
| x | 0 | 1 | 2 | 3 |
| y | 0 | 58 | 112 | 162 |
(2)求:销售到第几天结束时,该商品全部售完?
(3)若第m天的销量为22件,求m的值.
考点:二次函数的应用
专题:
分析:(1)根据表格得到两对x、y的值,代入二次函数的解析式即可确定a、b的值;
(2)将得到的二次函数的解析式配方后即可确定最值,从而确定售完时间;
(3)代入总销量22,从而得到有关m的方程,求得m的值即可.
(2)将得到的二次函数的解析式配方后即可确定最值,从而确定售完时间;
(3)代入总销量22,从而得到有关m的方程,求得m的值即可.
解答:解:(1)依题意,设y=ax2+bx(a≠0),则
,
解得:
.
故y与x之间的函数关系式为y=-2x2+60x.
(2)y=-2(x-15)2+450,
当x=15,
ymax=450.
答:销售到第15天结束,全部售完.
(3)当[-2(m-15)2+450]-[-2(m+15)2+450]=22时,
化简得:(m-16)2-(m-15)2=11,
解得:m=10.
|
解得:
|
故y与x之间的函数关系式为y=-2x2+60x.
(2)y=-2(x-15)2+450,
当x=15,
ymax=450.
答:销售到第15天结束,全部售完.
(3)当[-2(m-15)2+450]-[-2(m+15)2+450]=22时,
化简得:(m-16)2-(m-15)2=11,
解得:m=10.
点评:本题考查了二次函数的应用,解题的关键是从实际问题中抽象出二次函数的模型,难度不大.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
一个钝角三角形的两边长为3、4,则第三边可以为( )
| A、4 | B、5 | C、6 | D、7 |
若M-(-1)2+
=2,则M=( )
| -1×(-1)3-2 |
| 2×(-1)+1 |
| A、-2 | B、-1 | C、1 | D、2 |
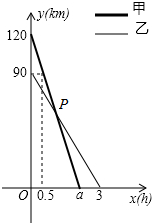 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图,请回答下列问题:
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图,请回答下列问题: