题目内容
8.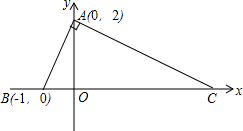 如图,平面直角坐标系中,AB⊥AC,
如图,平面直角坐标系中,AB⊥AC,(1)求点C的坐标;
(2)求Rt△BAC的周长.
分析 (1)证明Rt△ABO∽Rt△CAO,利用相似比计算出OC=4,于是可得到点C的坐标为(4,0);
(2)先利用勾股定理计算出AB和AC,而BC=5,然后根据三角形周长的定义求解.
解答 解:(1)∵AB⊥AC,
∴∠BAC=90°,即∠BAO+∠CAO=90°,
而∠BAO+∠ABO=90°,
∴∠CAO=∠ABO,
∴Rt△ABO∽Rt△CAO,
∴$\frac{OA}{OC}$=$\frac{OB}{OA}$,即$\frac{2}{OC}$=$\frac{1}{2}$,
∴OC=4,
∴点C的坐标为(4,0);
(2)在Rt△AOB中,AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
在Rt△AOC中,AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
BC=4-(-1)=5,
所以Rt△BAC的周长=AB+AC+BC=$\sqrt{5}$+2$\sqrt{5}$+5=3$\sqrt{5}$+5.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了坐标与图形性质.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 如图,已知△ABC:
如图,已知△ABC: 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1). 已知:在平面直角坐标系xoy中,抛物线y=ax2+bx+c与直线y=mx+n相交于
已知:在平面直角坐标系xoy中,抛物线y=ax2+bx+c与直线y=mx+n相交于 如图,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE,请你判断AC垂直于CE吗?并说明理由.
如图,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE,请你判断AC垂直于CE吗?并说明理由.