题目内容
6. 已知等腰三角形的周长为12cm,腰长y(cm)是底边长x(cm)的函数.
已知等腰三角形的周长为12cm,腰长y(cm)是底边长x(cm)的函数.(1)写出这个函数关系式;
(2)求自变量的取值范围;
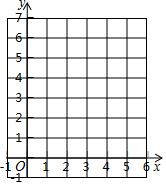
(3)在如图的直角坐标系中画出这个函数的图象.
分析 (1)根据底边长=周长-2×腰长即可写出这个函数关系式;
(2)根据三角形三边关系定理:三角形任意两边之和大于第三边来进行解答.
(3)由(1)、(2)即可得出y关于x的函数关系式(带自变量的取值范围),将其在坐标系中画出来即可.
解答 解:(1)依题意有:y=12-2x,
故y与x的函数关系式为:y=12-2x;
(2)依题意有:$\left\{\begin{array}{l}{2x>y}\\{x+y>x}\end{array}\right.$,
即$\left\{\begin{array}{l}{2x>12-2x}\\{12-2x>0}\end{array}\right.$,
解得:3<x<6.
故自变量x的取值范围为3<x<6.
(3)在直角坐标系中将其画出来,如图所示.
点评 本题考查了等腰三角形的性质、三角形的三边关系以及解一元一次不等式组,解题的关键是根据三角形的三边关系找出关于x的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据三角形的周长公式找出函数关系式是关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
17.下列说法正确的是( )
| A. | 有一组对角是直角的四边形一定是矩形 | |
| B. | 对角线互相平分的四边形是矩形 | |
| C. | 有一组邻角是直角的四边形一定是矩形 | |
| D. | 对角互补的平行四边形是矩形 |
11.下列图形中,对称轴数量最多的是( )
| A. |  | B. |  | C. |  | D. |  |
15.在估算一元二次方程x2+12x-15=0的根时,小彬列表如下:
由此可估算方程x2+12x-15=0的一个根x的范围是1.1<x<1.2.
| x | 1 | 1.1 | 1.2 | 1.3 |
| x2+12x-15 | -2 | -0.59 | 0.84 | 2.29 |
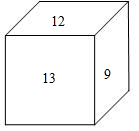 如图,一个正方体,6个面上分别写着6个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为9、12、13,则六个整数之和为69.
如图,一个正方体,6个面上分别写着6个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为9、12、13,则六个整数之和为69.