题目内容
1.已知实数a,b,c,d满足2a2+3c2=2b2+3d2=(ad-bc)2=6,求:(a2+b2)(c2+d2)的值.分析 由2a2+3c2=2b2+3d2=6得4a2b2+6a2d2+6b2c2+9c2d2=36,由a2d2-2abcd+b2c2=6得a2d2+b2c2=6+2abcd,从而有6a2d2+6b2c2=36+12abcd,即2ab=-3cd ①,结合2(a2-b2)=-3(c2-d2)②,①×②得(ac+bd)(ad-bc)=0,知ac+bd=0,代入原式=(ac+bd)2+(ad-bc)2可得答案.
解答 解:∵2a2+3c2=2b2+3d2=6,
∴(2a2+3c2)(2b2+3d2)=36,即4a2b2+6a2d2+6b2c2+9c2d2=36,
∵(ad-bc)2=6,
∴a2d2-2abcd+b2c2=6,即a2d2+b2c2=6+2abcd,
∴6a2d2+6b2c2=36+12abcd,
∴4a2b2+36+12abcd+9c2d2=36,即(2ab+3cd)2=0,
∴2ab=-3cd ①,
由2a2+3c2=2b2+3d2知2(a2-b2)=-3(c2-d2) ②,
①×②,得:-6cd(a2-b2)=-6ab(c2-d2),即cd(a2-b2)=ab(c2-d2),
a2cd-b2cd-abc2+abd2=0,
(ac+bd)(ad-bc)=0,
∵(ad-bc)2=6,
∴ad-bc≠0,
则ac+bd=0,
∴(a2+b2)(c2+d2)=a2c2+b2d2+a2d2+b2c2
=(ac+bd)2+(ad-bc)2
=02+6
=6.
点评 本题主要考查因式分解的应用,熟练掌握因式分解和整式的乘法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.抛物线y=5(x+2)2-3图象的顶点坐标是( )
| A. | (-3,-2) | B. | (2,3) | C. | (-2,3) | D. | (-2,-3) |
12.算式(-20)-(+3)-(+5)-(-7)写成省略加号的和的形式正确的为( )
| A. | 20+3+5-7 | B. | -20-3-5-7 | C. | -20-3+5+7 | D. | -20-3-5+7 |
9.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
设鸭的质量为x千克,烤制时间为t,估计当x=2.9千克时,t的值为136.
| 鸭的质量/千克 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 烤制时间/分 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
16.正六边形的外接圆半径为2,则它的内切圆半径为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 2 | D. | 1 |
13. 如图所示的圆柱,从左边看是( )
如图所示的圆柱,从左边看是( )
 如图所示的圆柱,从左边看是( )
如图所示的圆柱,从左边看是( )| A. |  | B. |  | C. |  | D. |  |
10.下列函数中,自变量x的取值范围为x>3的是( )
| A. | y=$\frac{1}{x-3}$ | B. | y=$\frac{1}{\sqrt{x-3}}$ | C. | y=x-3 | D. | y=$\sqrt{x-3}$ |
 已知等腰三角形的周长为12cm,腰长y(cm)是底边长x(cm)的函数.
已知等腰三角形的周长为12cm,腰长y(cm)是底边长x(cm)的函数.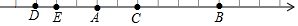 如下图,数轴上相邻刻度之间的距离是$\frac{1}{5}$,点A表示的数是$-\frac{4}{5}$,又知点B和点C表示的数互为相反数,则点E表示的有理数是-$\frac{6}{5}$,点D与点C之间相距1.
如下图,数轴上相邻刻度之间的距离是$\frac{1}{5}$,点A表示的数是$-\frac{4}{5}$,又知点B和点C表示的数互为相反数,则点E表示的有理数是-$\frac{6}{5}$,点D与点C之间相距1.