题目内容
19.若一次函数y1=(m2-4)x+4-2m2与一次函数y2=(m2-4)x+m2-3的图象与y轴交点的纵坐标互为相反数,则m=±1.分析 根据一次函数的定义即可得出m2-4≠0,即m≠±2,再根据一次函数图象上点的坐标特征结合两函数图象与y轴交点的纵坐标互为相反数,即可得出4-2m2+m2-3=0,解之即可得出结论.
解答 解:∵y1=(m2-4)x+4-2m2与y2=(m2-4)x+m2-3均为一次函数,
∴m2-4≠0,
∴m≠±2.
将x=0分别代入两函数解析式可求出两函数图象与y轴的交点坐标为(0,4-2m2)和(0,m2-3).
∵两函数图象与y轴交点的纵坐标互为相反数,
∴4-2m2+m2-3=0,
解得:m=±1.
故答案为:±1.
点评 本题考查了一次函数的定义、一次函数图象上点的坐标特征以及相反数,根据一次函数图象上点的坐标特征求出两函数图象与y轴的交点坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下面是小玲同学在一次课堂测验中利用等式的性质解方程的过程,其中正确的是( )
| A. | -$\frac{1}{3}$x-5=4,得$\frac{1}{3}$x=4+5 | B. | 5y-3y+y=9,得(5-3)y=9 | ||
| C. | x+7=26,得x=19 | D. | -5x=20,得x=-$\frac{5}{20}$ |
14.抛物线y=5(x+2)2-3图象的顶点坐标是( )
| A. | (-3,-2) | B. | (2,3) | C. | (-2,3) | D. | (-2,-3) |
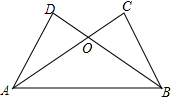 如图,已知AD=BC,AC=BD=10.
如图,已知AD=BC,AC=BD=10.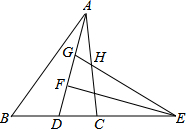 如图,在△ABC中,2AB=3AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H,若点H是AC的三等分点,则$\frac{AG}{GD}$为$\frac{2}{7}$或$\frac{4}{5}$..
如图,在△ABC中,2AB=3AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H,若点H是AC的三等分点,则$\frac{AG}{GD}$为$\frac{2}{7}$或$\frac{4}{5}$..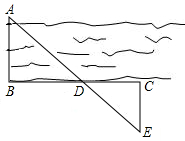 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=150米,DC=60米,EC=50米,试求两岸间的距离AB.
如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=150米,DC=60米,EC=50米,试求两岸间的距离AB. 如图,阴影部分是一个正方形,则此正方形的面积为多少cm2?
如图,阴影部分是一个正方形,则此正方形的面积为多少cm2? 已知等腰三角形的周长为12cm,腰长y(cm)是底边长x(cm)的函数.
已知等腰三角形的周长为12cm,腰长y(cm)是底边长x(cm)的函数.