题目内容
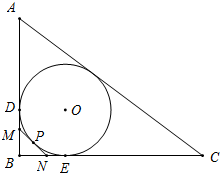 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=5cm,AC=13cm,则Rt△MBN的周长为
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=5cm,AC=13cm,则Rt△MBN的周长为考点:切线长定理
专题:
分析:根据勾股定理求出AC的长,再设△ABC内切圆的半径为R,切点分别为D、E、F,证明四边形ODBE是正方形,根据切线长定理得出结论即可.
解答:解:如图所示:连接DO,EO,
Rt△ABC中,AB=5cm,AC=13cm,则BC=12cm,
设△ABC内切圆的半径为R,切点分别为D、E、F,
∵AD=AF,BE=BD,CF=CE,
∵OD⊥AB,OE⊥BC,
∴四边形ODBE是正方形,即BD=BE=R,
∴AB-BD=AF,CB-BE=FC,
5-R+12-R=13,
解得:R=2,
∵切线MN与AB,BC分别交于点M,N,
∴MP=DM,PN=NE,
∴Rt△MBN的周长为:BD+BE=2+2=4(cm),
故答案为:4.
Rt△ABC中,AB=5cm,AC=13cm,则BC=12cm,
设△ABC内切圆的半径为R,切点分别为D、E、F,
∵AD=AF,BE=BD,CF=CE,

∵OD⊥AB,OE⊥BC,
∴四边形ODBE是正方形,即BD=BE=R,
∴AB-BD=AF,CB-BE=FC,
5-R+12-R=13,
解得:R=2,
∵切线MN与AB,BC分别交于点M,N,
∴MP=DM,PN=NE,
∴Rt△MBN的周长为:BD+BE=2+2=4(cm),
故答案为:4.
点评:本题考查了三角形的内切圆和内心以及勾股定理和切线长定理,是中考的常见题型,要熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知三角形的三边长的比是1:
:
,那么这个三角形一定不是( )
| ||
| 2 |
| 1 | ||
|
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、不等边三角形 |
 (1)已知a,b都是有理数,在数轴上的位置如图所示,则a,-b,|a|,|b|的大小关系是:
(1)已知a,b都是有理数,在数轴上的位置如图所示,则a,-b,|a|,|b|的大小关系是: 一架云梯长25米,如图所示,斜靠在一面墙上,这时梯子的顶端距地面24米.
一架云梯长25米,如图所示,斜靠在一面墙上,这时梯子的顶端距地面24米. 如图,在一个长为300米,宽为200米的长方形场地上修三条不同形状的小路,剩余部分作为绿化区种植花草.已知三条小路的边缘长都为x,让各条小路的两边分别平行.若绿化面积为53200平方米,求小路的边缘长x.
如图,在一个长为300米,宽为200米的长方形场地上修三条不同形状的小路,剩余部分作为绿化区种植花草.已知三条小路的边缘长都为x,让各条小路的两边分别平行.若绿化面积为53200平方米,求小路的边缘长x.