Question

14．如图，△ABC为等边三角形，BD平分∠ABC，DE∥BC．
（1）求证：△ADE是等边三角形；
（2）求证：AE=$\frac{1}{2}$AB．

Answer 1

分析 （1）根据等边三角形的判定证明即可；
（2）利用等边三角形的性质解答即可．

解答 证明：（1）∵△ABC为等边三角形，
∴∠A=∠ABC=∠ACB=60°，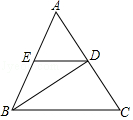

∵DE∥BC，
∴∠AED=∠ABD=60°，
∴∠ADE=∠ACB=60°，
∴∠A=∠AED=∠ADE，
∴△ADE是等边三角形；
（2）∵△ADE是等边三角形
∴AD=AE　　　　
∵△ABC为等边三角形，
∴AB=AC　
∵BD平分∠ABC，
∴D是AC的中点（三线合一）
AD=$\frac{1}{2}$AC=$\frac{1}{2}$AB，
∴AE=$\frac{1}{2}$AB．

点评 本题考查了等边三角形性质，相似三角形的判定，平行线的性质等知识点的应用，关键是推出AB=BC=AC，此题题型较好，证法不一，如证∠A=∠B=∠C或根据一个角是60°的等腰三角形是等边三角形去证．