题目内容
10.如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=-x2+4x+2的一部分,曲线BC是双曲线y=$\frac{k}{x}$的一部分,由点C开始不断重复“A-B-C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )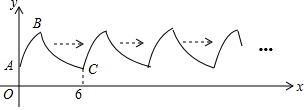
| A. | 72 | B. | 36 | C. | 16 | D. | 9 |
分析 A,C之间的距离为6,点Q与点P的水平距离为8,抛物线的顶点B的坐标为(2,6),进而得到A,B之间的水平距离为6,且k=12,根据四边形P'M'N'Q'的面积为$\frac{8(4+5)}{2}$=36,即可得到四边形PMNQ的面积为36.
解答 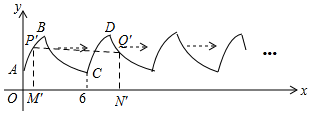 解:如图所示,A,C之间的距离为6,
解:如图所示,A,C之间的距离为6,
2017÷6=336…1,故点P离x轴的距离与点P'离x轴的距离相同,
在y=-x2+4x+2中,当x=1时,y=5,即点P'离x轴的距离为5,
∴P'M'=5,
2025-2017=8,故点Q与点P的水平距离为8,
即M'N'=MN=8,点Q离x轴的距离与点Q'离x轴的距离相同,
由题可得,抛物线的顶点B的坐标为(2,6),故A,B之间的水平距离为6,且k=12,
∵点D与点Q'的水平距离为1+8-6-2=1,点C与点Q'的水平距离为1+2=3,
∴在y=$\frac{12}{x}$中,当x=3时,y=4,即点Q'离x轴的距离为4,
∴Q'N'=4,
∵四边形P'M'N'Q'的面积为$\frac{8(4+5)}{2}$=36,
∴四边形PMNQ的面积为36,
故选:B.
点评 本题主要考查了反比例函数图象上的点的坐标特征以及二次函数的性质,解题时注意:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$;四边形PMNQ为梯形,依据梯形的面积公式即可得到其面积.

练习册系列答案
相关题目
14. 如图,已知直线a,b,c相交于点O,∠1=45°,则∠2的度数为( )
如图,已知直线a,b,c相交于点O,∠1=45°,则∠2的度数为( )
 如图,已知直线a,b,c相交于点O,∠1=45°,则∠2的度数为( )
如图,已知直线a,b,c相交于点O,∠1=45°,则∠2的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
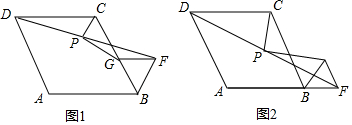
 已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.
已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.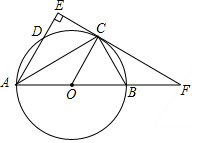 如图,⊙O是以AB为直径的圆,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点F,连结CA,CB.
如图,⊙O是以AB为直径的圆,C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点F,连结CA,CB.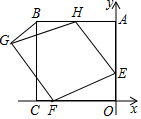 如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.
如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH. 实践与操作:
实践与操作: