题目内容
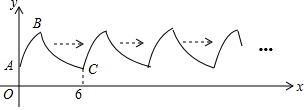
20. 已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.
已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.(1)若DF=2,求AB的长;
(2)若AB=18时,等边△CDP和△EFP的面积之和是否有最大值,如果有最大值,求最大值及此时P点位置,若没有最大值,说明理由.
分析 (1)由等边三角形的性质容易得出结果;
(2)设CD=PC=PD=x,则EF=EP=PF=6-x,求出等边△CDP和△EFP的面积之和S=$\frac{\sqrt{3}}{2}$x2-3$\sqrt{3}$x+9$\sqrt{3}$,$\frac{\sqrt{3}}{2}$>0,得出S有最小值,没有最大值.
解答 解:(1)∵△CDP和△EFP是等边三角形,
∴CD=PC=PD,EF=EP=PF,AP=3PD,BP=3PF,
∵DF=PD+PF=2,
∴AB=AP+BP=3DF=3×2=6;
(2)没有最大值,理由如下:
设CD=PC=PD=x,则EF=EP=PF=$\frac{1}{3}$(18-3x)=6-x,
作CM⊥PD于M,EN⊥PF于N,
则DM=$\frac{1}{2}$PD=$\frac{1}{2}$x,PN=$\frac{1}{2}$PF=$\frac{1}{2}$(6-x),
∴CM=$\sqrt{3}$DM=$\frac{\sqrt{3}}{2}$x,EN=$\frac{\sqrt{3}}{2}$(6-x),
∴△CDP的面积=$\frac{1}{2}$PD•CM=$\frac{\sqrt{3}}{4}$x2,△EFP的面积=$\frac{\sqrt{3}}{4}$(6-x)2,
∴等边△CDP和△EFP的面积之和S=$\frac{\sqrt{3}}{4}$x2+$\frac{\sqrt{3}}{4}$(6-x)2=$\frac{\sqrt{3}}{2}$x2-3$\sqrt{3}$x+9$\sqrt{3}$,
∵$\frac{\sqrt{3}}{2}$>0,
∴S有最小值,没有最大值.
点评 本题考查了翻折变换的性质、等边三角形的性质、二次函数的最值等知识;熟练掌握翻折变换和等边三角形的性质是解决问题的关键.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案| A. | 0或$\frac{1}{2}$ | B. | -1 | C. | -2 | D. | -3 |
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是正方形 | |
| C. | 一组对边平行的四边形是平行四边形 | |
| D. | 四边相等的四边形是菱形 |