Question

18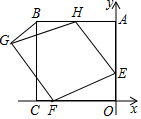．如图，在平面直角坐标系中，正方形ABCD的顶点C、A分别在x、y轴上，A（0，6），E（0，2），点H、F分别在边AB、OC上，以H、E、F为顶点作菱形EFGH．
（1）当H（-2，6）时，求证：四边形EFGH是正方形；
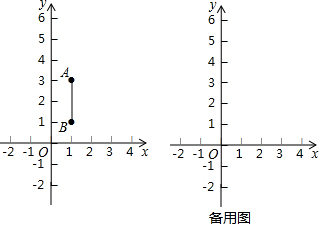
（2）若F（-5，0），求点G的坐标．

Answer 1

分析 （1）只要证明Rt△AHE≌Rt△OEF，推出∠AEH=∠EFO，由∠EFO+∠FEO=90°，推出∠AEH+∠FEO=90°，推出∠HEF=90°，即可证明．
（2）连接EG交FH于K．首先求出点H的坐标，利用中点坐标公式求出K的坐标，再求出点G坐标即可．

解答 解：（1）∵四边形ABCD是正方形，
∴∠BAO=∠AOC=90°，
∵E（0，2），H（-2，6），
∴AH=OE=2，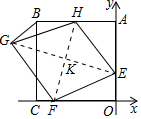
∵四边形EFGH是菱形，
∴EH=EF，
在Rt△AHE和Rt△OEF中，
$\left\{\begin{array}{l}{EH=EF}\\{AH=OE}\end{array}\right.$，
∴Rt△AHE≌Rt△OEF，
∴∠AEH=∠EFO，
∵∠EFO+∠FEO=90°，
∴∠AEH+∠FEO=90°，
∴∠HEF=90°，∵四边形EFGH是菱形，
∴四边形EFGH是正方形．

（2）连接EG交FH于K．
∵HE=EF，
∴AH²+AE²=EO²+OF²，
∴AH²+16=4+25，
∴AH=$\sqrt{13}$，
∴H（-$\sqrt{13}$，6），
∵KH=KF，
∴K（-$\frac{5+\sqrt{13}}{2}$，3），
∵GK=KE，
∴G（-5-$\sqrt{13}$，4）．

点评 本题考查正方形的性质和判定、菱形的性质、勾股定理、中点坐标公式等知识，解题的关键是正确寻找全等三角形解决问题，学会利用中点坐标公式，属于中考常考题型．