题目内容
2．
如图，⊙O是Rt△ABC的内切圆，∠C=90°，BO的延长线交AC于点D，若BC=4，CD=2，则⊙O的半径的值是$\frac{4}{3}$．
分析 设半径为r 过点O作OE⊥BC，垂足为E．再根据△BCD∽△BOE，然后根据对应边成比例，解出r即可．
解答 解：设半径为r 过点O作OE⊥BC，垂足为E，如图所示：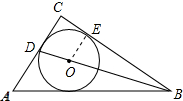
∵OE∥AC，
∴△BCD∽△BEO，
由题意可得出：OE=EC=r，
∴$\frac{BE}{BC}=\frac{EO}{CD}$，即$\frac{4-r}{4}=\frac{r}{2}$，
解得：r=$\frac{4}{3}$，
故答案为：$\frac{4}{3}$．
点评 此题主要考查了三角形内心的性质、相似三角形的判定与性质；得出EO=EC=r是解题关键．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
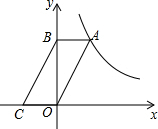如图，在平面直角坐标系中，点A在函数y=$\frac{k}{x}（k＞0，x＞0）$的图象上，过点A作AB∥x轴交y轴于点B，连结OA，过点B作BC∥OA交x轴于点C，若△BOC的面积是2，则k=4．
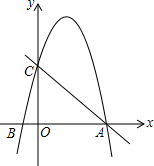如图，平面直角坐标系xOy中，已知B（-1，0），一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点，二次函数y=-x2+bx+c的图象经过点A、点B．
17．一组数据7，2，5，4，2的方差为a，若再增加一个数据4，这6个数据的方差为b，则a与b的大小关系是（ ）
| A． | a＞b | B． | a=b | C． | a＜b | D． | 以上都有可能 |