题目内容
12.人民商场销售某种冰箱,每台进价为2500元,市场调研表明:当每台销售价定为2900元时,平均每天能售出8台;每台售价每降低50元,平均每天能多售出4台.设该种冰箱每台的销售价降低了x元.
(1)填表:
| 每天售出的冰箱台数(台) | 每台冰箱的利润(元) | |
| 降价前 | 8 | 400 |
| 降价后 | 8+$\frac{x}{50}$×4 | 400-x |
分析 (1)销售利润=一台冰箱的利润×销售冰箱数量,一台冰箱的利润=售价-进价,降低售价的同时,销售量就会提高,“一减一加”;
(2)根据每台的盈利×销售的件数=5000元,即可列方程求解.
解答 解:(1)销售1台的利润:2900-2500=400;
降价后销售的数量:8+$\frac{x}{50}$×4,
降价后销售的利润:400-x;
故答案是:400;8+$\frac{x}{50}$×4,400-x.
(2)设销售价降低了x元,根据题意可得:
(400-x)•(8+$\frac{x}{50}$×4)=5000,
整理得:x2-300x+22500=0,
(x-150)2=0,
解得:x1=x2=150,
2900-150=2750(元),
答:每台冰箱的售价应定为2750元.
点评 此题主要考查了一元二次方程的应用,本题关键是会表示一台冰箱的利润,销售量增加的部分.找到关键描述语,找到等量关系:每台的盈利×销售的件数=5000元是解决问题的关键.

练习册系列答案
相关题目
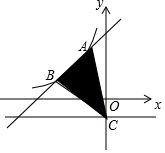 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x<0)的图象交于A(-1,3),B(-3,n)两点,直线y=-1与y轴交于点C.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x<0)的图象交于A(-1,3),B(-3,n)两点,直线y=-1与y轴交于点C.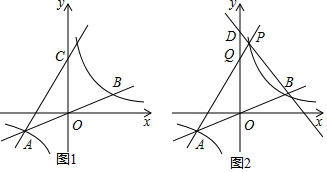
 解不等式组$\left\{\begin{array}{l}{2(x+1)≥0,①}\\{1-\frac{x}{3}>\frac{x-3}{6},②}\end{array}\right.$并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{2(x+1)≥0,①}\\{1-\frac{x}{3}>\frac{x-3}{6},②}\end{array}\right.$并把解集在数轴上表示出来. 如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
如图所示,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.