题目内容
7.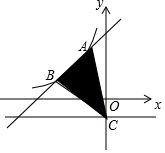 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x<0)的图象交于A(-1,3),B(-3,n)两点,直线y=-1与y轴交于点C.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x<0)的图象交于A(-1,3),B(-3,n)两点,直线y=-1与y轴交于点C.(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
分析 (1)先把点A坐标代入反比例函数解析式,求得m,再把点B坐标代入即可得出n,再由待定系数法得出答案;
(2)用长方形的面积减去三角形的面积即可得出答案.
解答 解:(1)反比例函数y=$\frac{m}{x}$(x<0)的图象经过点A(-1,3),
∴m=-3,
∴反比例函数的解析式为y=-$\frac{3}{m}$,
∵点B(-3,n)在反比例函数的y=-$\frac{3}{x}$ 图象上,
∴n=1,
∴B(-3,1);
∵一次函数y=kx+b的图象经过A(-1,3).B(-3,1)两点
∴$\left\{\begin{array}{l}{-k+b=3}\\{-3k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=4}\end{array}\right.$,
∴一次函数的解析式是y=x+4;
(2)S△ABC=3×4-$\frac{1}{2}$×2×2-$\frac{1}{2}$×1×4-$\frac{1}{2}$×3×2
=12-2-2-3
=5.
点评 本题考查了用待定系数法求一次函数的解析式和反比例函数的解析式,掌握三角形面积的求法是解题的关键.

练习册系列答案
相关题目
18.经市场调查,某种商品在第x天(1≤x≤90)的售价与销量的相关信息如下表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(I)分别求出当1≤x<60和60≤x≤90时,该商品每天利润y与x之间的函数表达式.
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少元?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
| 时间x(天) | 1≤x≤60 | 60≤x≤90 |
| 售价(元/件) | x+40 | 100 |
| 每天销量(件) | 200-2x | |
(I)分别求出当1≤x<60和60≤x≤90时,该商品每天利润y与x之间的函数表达式.
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少元?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
12.人民商场销售某种冰箱,每台进价为2500元,市场调研表明:当每台销售价定为2900元时,平均每天能售出8台;每台售价每降低50元,平均每天能多售出4台.
设该种冰箱每台的销售价降低了x元.
(1)填表:
(2)若商场要想使这种冰箱的销售利润平均每天达到5000元,则每台冰箱的售价应定为多少元?
设该种冰箱每台的销售价降低了x元.
(1)填表:
| 每天售出的冰箱台数(台) | 每台冰箱的利润(元) | |
| 降价前 | 8 | 400 |
| 降价后 | 8+$\frac{x}{50}$×4 | 400-x |
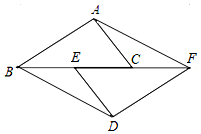 如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC. 如图所示,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=56°,∠E=32°,则∠F=36°.
如图所示,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=56°,∠E=32°,则∠F=36°. △ABC中,D、E分别在AB、AC上,DE∥BC,AD=1,BD=3,则△ADE与△ABC的面积之比为1:16.
△ABC中,D、E分别在AB、AC上,DE∥BC,AD=1,BD=3,则△ADE与△ABC的面积之比为1:16. 如图,点A为⊙O上的一点,请用尺规作⊙O的内接正六边形ABCDEF(不写作法,但须保留作图痕迹).
如图,点A为⊙O上的一点,请用尺规作⊙O的内接正六边形ABCDEF(不写作法,但须保留作图痕迹).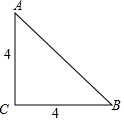 如图,在等腰直角三角形ABC纸片中,以C为圆心,剪出一个面积最大的扇形,制作圆锥模型,则此圆锥模型的底面半径为$\frac{\sqrt{2}}{2}$.
如图,在等腰直角三角形ABC纸片中,以C为圆心,剪出一个面积最大的扇形,制作圆锥模型,则此圆锥模型的底面半径为$\frac{\sqrt{2}}{2}$.