题目内容
2.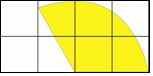 在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$.
在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$.
分析 分别计算此扇形的弧长和侧面积后即可得到结论.
解答  解:如图,∵AO=2,0C=1,
解:如图,∵AO=2,0C=1,
∴∠AOC=60°,
∴∠AOB=120°,
∴$\widehat{AB}$的长度=$\frac{120•π×2}{180}$=$\frac{4}{3}$π,
设所围成的圆锥的底面圆的半径为r,
∴$\frac{4}{3}$π=2πr,
∴r=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查了圆锥的计算及弧长的计算的知识,解题的关键是能够从图中了解到扇形的弧长和扇形的半径并利用扇形的有关计算公式进行计算,难度不大.

练习册系列答案
相关题目
10. 如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )
如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )
 如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )
如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )| A. | 88° | B. | 30° | C. | 32° | D. | 48° |
17.在下列图形中,是中心对称图形而不是轴对称图形的是( )
| A. | 圆 | B. | 等边三角形 | C. | 梯形 | D. | 平行四边形 |
11.如果a>b、c<0,那么下列不等式成立的是( )
| A. | c-a>c-b | B. | a+c>b+c | C. | ac>bc | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
 我国古代数学家利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
我国古代数学家利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )


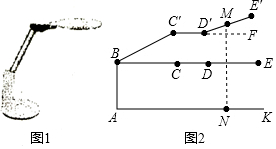 市场上一款护眼灯(如图1),采用圆形面光源技术,胡烈其旋转支架等的宽度,得到它的侧面简化结构图(如图2),底座AB⊥桌面AK,旋转支架BC可绕点B旋转,转接头CD∥桌面AK,圆形面光源在旋转支架所在平面捏可绕点D旋转,其直径DE为20cm,若旋转支架旋转至BC′处,圆形面光源DE旋转至D′E′处,此时圆形面光源中心M到桌面的距离MN=40cm,已知AB=20cm,∠CBC=37°,∠E′D′F=24°,则旋转支架BC长为( )cm(结果精确到1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
市场上一款护眼灯(如图1),采用圆形面光源技术,胡烈其旋转支架等的宽度,得到它的侧面简化结构图(如图2),底座AB⊥桌面AK,旋转支架BC可绕点B旋转,转接头CD∥桌面AK,圆形面光源在旋转支架所在平面捏可绕点D旋转,其直径DE为20cm,若旋转支架旋转至BC′处,圆形面光源DE旋转至D′E′处,此时圆形面光源中心M到桌面的距离MN=40cm,已知AB=20cm,∠CBC=37°,∠E′D′F=24°,则旋转支架BC长为( )cm(结果精确到1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)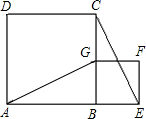 如图,正方形BEFG的边BG在正方形ABCD的边BC上,连结AG,EC.
如图,正方形BEFG的边BG在正方形ABCD的边BC上,连结AG,EC. 如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,点F在线段AG上,且BF∥DE.
如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,点F在线段AG上,且BF∥DE.