题目内容
10. 如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )
如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )| A. | 88° | B. | 30° | C. | 32° | D. | 48° |
分析 先根据角平分线的定义,得到∠COF=30°,∠AOC=2∠COE,再根据∠AOC+∠EOF=156°,可得2∠COE+∠COE-30°=156°,求得∠COE=62°,进而得到∠EOF的度数.
解答 解:∵OF平分∠BOC,∠BOC=60°,
∴∠COF=30°,
∴∠EOF=∠COE-∠COF=∠COE-30°,
∵OE平分∠AOC,
∴∠AOC=2∠COE,
又∵∠AOC+∠EOF=156°,
∴2∠COE+∠COE-30°=156°,
解得∠COE=62°,
∴∠EOF=62°-30°=32°.
故选:C.
点评 本题考查了角的计算以及角平分线的定义,解题的关键是根据角平分线的定义以及角的和差关系进行计算.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
18.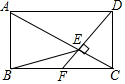 如图,在矩形ABCD中,F是BC边的中点,DF⊥AC,垂足为点E,连接BE,分析下列四个结论:①△CEF∽△CBA;②BE=AB;③AE=2CE;④tan∠ACB=$\sqrt{2}$,其中正确的个数有( )
如图,在矩形ABCD中,F是BC边的中点,DF⊥AC,垂足为点E,连接BE,分析下列四个结论:①△CEF∽△CBA;②BE=AB;③AE=2CE;④tan∠ACB=$\sqrt{2}$,其中正确的个数有( )
 如图,在矩形ABCD中,F是BC边的中点,DF⊥AC,垂足为点E,连接BE,分析下列四个结论:①△CEF∽△CBA;②BE=AB;③AE=2CE;④tan∠ACB=$\sqrt{2}$,其中正确的个数有( )
如图,在矩形ABCD中,F是BC边的中点,DF⊥AC,垂足为点E,连接BE,分析下列四个结论:①△CEF∽△CBA;②BE=AB;③AE=2CE;④tan∠ACB=$\sqrt{2}$,其中正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
19.下列4个数中,3.1415926,$\frac{22}{7}$,π,$\sqrt{36}$,其中无理数是( )
| A. | 3.1415926 | B. | $\frac{22}{7}$ | C. | π | D. | $\sqrt{36}$ |

 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东45°的方向,请求出海岛C到航线AB的距离(结果保留根号).
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东45°的方向,请求出海岛C到航线AB的距离(结果保留根号). 如图,C、D为线段AB上的两点,M是AC的中点,N是BD的中点.如果MN=a,CD=b,求线段AB的长(用a、b的代数式表示).
如图,C、D为线段AB上的两点,M是AC的中点,N是BD的中点.如果MN=a,CD=b,求线段AB的长(用a、b的代数式表示).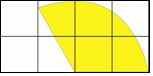 在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$.
在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$.