题目内容
12. 如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,点F在线段AG上,且BF∥DE.
如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,点F在线段AG上,且BF∥DE.(1)猜想线段DE、BF、EF之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为2,将△ABF绕点A逆时针旋转90°,点F的对应点为F′,请补全图形,并求出E、F′两点间的距离.
分析 (1)本题的关键是求△ADE和ABF全等,以此来得出DE=AF=AE+EF=BE+EF,这两个三角形中已知的条件有AD=BA,一组直角,关键是再找出一组对应角相等,可通过证明∠DAF和∠ABF来实现,
(2)由(1)得到BF=AE,AF=DE,由旋转得,AF=AF′,BF=DF′,判断出四边形AEDF′是矩形即可.
解答 (1)证明:∵四边形ABCD是正方形,BF⊥AG,DE⊥AG,
∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,$\left\{\begin{array}{l}{∠BAF=∠ADE}\\{∠AFB=∠DEA}\\{AB=AD}\end{array}\right.$,
∴△ABF≌△DAE,
∴BF=AE,AF=DE,
∴DE-BF=AF-AE=EF.
(2)解:如图①,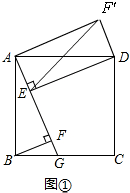
理由如下:
由(1)有,BF=AE,AF=DE,
由旋转得,AF=AF′,BF=DF′,
∴AE=DF′,DE=AF′,
∴四边形AEDF′是平行四边形,
∵DE⊥AG,
∴∠AED=90°,
∴四边形AEDF′是矩形,
∴EF′=AD=2.
点评 此题主要考查了正方形的性质和垂直的意义,全等三角形的性质和判定,解答本题的关键是熟练掌握有两组角对应相等的两个三角形相似;两组边对应成比例且夹角相等的三角形相似.

练习册系列答案
相关题目
3.一个多边形的内角和大于1100°,小于1400°这个多边形的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
20.在$\frac{xy}{2}$、$\frac{1}{x}$、$\frac{a}{4}$、$\frac{5}{π}$、$\frac{3}{x+y}$中分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.已知a>b,下列不等式中,不一定成立的是( )
| A. | a-5>b-5 | B. | $\frac{1}{2}$a>$\frac{1}{2}$b | C. | 2-3a<2-3b | D. | ma>mb |
4.已知x-2y=3,则代数式6-2x+4y的值为( )
| A. | -3 | B. | -1 | C. | 0 | D. | 3 |
1.若x+$\frac{1}{x}$=2,则x2+$\frac{1}{x^2}$=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
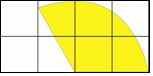 在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$.
在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$. 如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件∠AEF=∠BAD或∠CFE=∠BAC,使EF∥AB.
如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件∠AEF=∠BAD或∠CFE=∠BAC,使EF∥AB.