题目内容
7.OC,OD是分别从∠AOB的顶点O引出的两条射线,若∠AOB=75°,∠COB=45°并且OD平分∠AOC,试求∠BOD的度数.
分析 分两种情况进行讨论:当OC在∠AOB内部时,∠AOC=∠AOB-∠BOC=75°-45°=30°;当OC在∠AOB外部时,∠AOC=∠AOB+∠BOC=75°+45°=120°,分别根据角平分线的定义以及角的和差关系进行计算即可.
解答 解:当OC在∠AOB内部时,∠AOC=∠AOB-∠BOC=75°-45°=30°,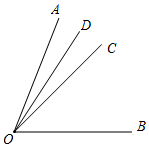
∵OD平分∠AOC,
∴∠COD=$\frac{1}{2}$∠AOC=15°,
∴∠BOD=∠BOC+∠COD=45°+15°=60°;
当OC在∠AOB外部时,∠AOC=∠AOB+∠BOC=75°+45°=120°,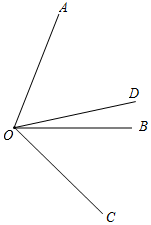
∵OD平分∠AOC,
∴∠COD=$\frac{1}{2}$∠AOC=60°,
∴∠BOD=∠COD-∠BOC=60°-45°=15°,
综上所述,∠BOD的度数为60°或15°.
点评 此题主要考查了角平分线的性质以及分类讨论思想的应用,根据射线OC在∠AOB外部或内部分类讨论是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.以下问题,不适合用全面调查的是( )
| A. | 旅客上飞机前的安检 | B. | 学校招聘教师,对应聘人员的面试 | ||
| C. | 了解全校学生的课外读书时间 | D. | 了解全国中学生的用眼卫生情况 |
19.下列4个数中,3.1415926,$\frac{22}{7}$,π,$\sqrt{36}$,其中无理数是( )
| A. | 3.1415926 | B. | $\frac{22}{7}$ | C. | π | D. | $\sqrt{36}$ |
16.下列计算正确的是( )
| A. | 3x2-2x2=1 | B. | (x2)3=x6 | C. | x8÷x4=x2 | D. | x3•x4=x12 |

 如图,C、D为线段AB上的两点,M是AC的中点,N是BD的中点.如果MN=a,CD=b,求线段AB的长(用a、b的代数式表示).
如图,C、D为线段AB上的两点,M是AC的中点,N是BD的中点.如果MN=a,CD=b,求线段AB的长(用a、b的代数式表示).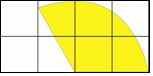 在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$.
在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$.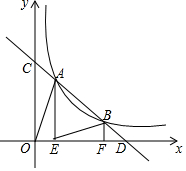 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上(点A在点B的左侧),直线AB分别交x轴,y轴于点D,C,AE⊥x轴于点E,BF⊥x轴于点F,连结AO,BE,已知AB=2BD,△AOC与△BDF的面积之和是△ABE的面积的k倍,则k的值是$\frac{5}{6}$.
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上(点A在点B的左侧),直线AB分别交x轴,y轴于点D,C,AE⊥x轴于点E,BF⊥x轴于点F,连结AO,BE,已知AB=2BD,△AOC与△BDF的面积之和是△ABE的面积的k倍,则k的值是$\frac{5}{6}$. 如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件∠AEF=∠BAD或∠CFE=∠BAC,使EF∥AB.
如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件∠AEF=∠BAD或∠CFE=∠BAC,使EF∥AB.