题目内容
12. 在平面直角坐标系中,已知点A(8,0)、B(0,6),以AB为边在第一象限内作等腰直角三角形ABC,则另一顶点C的坐标为(7,7),(14,8),(6,14).
在平面直角坐标系中,已知点A(8,0)、B(0,6),以AB为边在第一象限内作等腰直角三角形ABC,则另一顶点C的坐标为(7,7),(14,8),(6,14).
分析 分CA=CB、BC=BA、AC=AB三种情况,通过构建全等三角形得出点C的横纵坐标即可得答案.
解答 解:①如图1,过点C作CD⊥OA于D,CE⊥OB于E.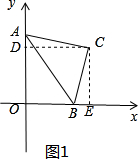
∵∠BCA=∠DCE=90°,
在△ACD与△BCE中,
∵$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠BCE}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△BCE,
∴BE=AD,CE=CD=OE,
∵AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴BC=$\frac{\sqrt{2}}{2}$AB=5$\sqrt{2}$,
CE2+(CE-6)2=BC2=50,
解得CE=7或-1(不合题意舍去).
则点C坐标为(7,7);
②如图2,过点B作BC⊥BA,使BC=BA,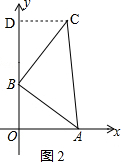
∴∠ABC=90°,
∴∠ABO+∠CBD=90°,
过点C作CD⊥y轴于点D,
∴∠AOB=∠BDC,∠BCD+∠CBD=90°,
∴∠ABO=∠BCD,
在△ABO和△BCD中,
∵$\left\{\begin{array}{l}{∠AOB=∠BDC}\\{∠ABO=∠BCD}\\{AB=BC}\end{array}\right.$,
∴△ABO≌△BCD,
∴CD=BO=6,BD=AO=8,
则OD=BO+BD=14,
∴点C(6,14);
③如图3,过点A作AC⊥AB,使AC=AB,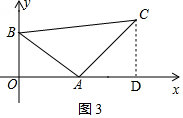
∴∠BAC=90°,
∴∠BAO+∠CAD=90°,
过点C作CD⊥x轴于点D,
∴∠AOB=∠CDA=90°,∴∠ACD+∠CAD=90°,
∴∠BAO=∠ACD,
在△ABO和△CAD中,
∵$\left\{\begin{array}{l}{∠AOB=∠CDA}\\{∠BAO=∠ACD}\\{AB=CA}\end{array}\right.$,
∴△ABO≌△CAD,
∴AD=BO=6,CD=OA=8,
则OD=OA+AD=14,
∴点C的坐标为(14,8),
综上,点C的坐标为(7,7),(14,8),(6,14),
故答案为:(7,7),(14,8),(6,14).
点评 本题主要考查全等三角形的判定与性质及等腰直角三角形的性质,作出辅助线构建全等三角形是本题的关键,并注意分类思想的运用.

 阅读快车系列答案
阅读快车系列答案| A. | 2016×103 | B. | 2.016×106 | C. | 2.016×107 | D. | 0.2016×107 |
| A. | 1cm | B. | $\sqrt{2}$cm | C. | $\sqrt{3}$cm | D. | 3cm |
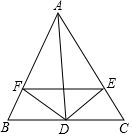 如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )
如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
| A. | 2a2+3a2=5a4 | B. | (3ab3)2=9a2b6 | C. | 2a6÷a3=2a2 | D. | (a2)3=a5 |
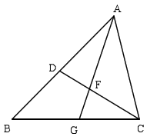 已知:如图,在△ABC中,点D、G分别在边AB、BC上,∠ACD=∠B,AG与CD相交于点F.
已知:如图,在△ABC中,点D、G分别在边AB、BC上,∠ACD=∠B,AG与CD相交于点F. 如图,已知数轴上的点A对应的数是a,点B对应的数是b,且满足(a+5)2+|b-1|=0
如图,已知数轴上的点A对应的数是a,点B对应的数是b,且满足(a+5)2+|b-1|=0