题目内容
17.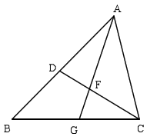 已知:如图,在△ABC中,点D、G分别在边AB、BC上,∠ACD=∠B,AG与CD相交于点F.
已知:如图,在△ABC中,点D、G分别在边AB、BC上,∠ACD=∠B,AG与CD相交于点F.(1)求证:AC2=AD•AB;
(2)若$\frac{AD}{AC}$=$\frac{DF}{CG}$,求证:CG2=DF•BG.
分析 (1)证明△ACD∽△ABC,得出对应边成比例AC:AB=AD:AC,即可得出结论;
(2)由相似三角形的性质得出∠ADF=∠ACG,由已知证出△ADF∽△ACG,得出∠DAF=∠CAF,AG是∠BAC的平分线,由角平分线得出$\frac{AC}{AB}=\frac{CG}{BG}$,即可得出结论.
解答 (1)证明:∵∠ACD=∠B,∠CAD=∠BAC,
∴△ACD∽△ABC,
∴AC:AB=AD:AC,
∴AC2=AD•AB;
(2)证明:∵△ACD∽△ABC,
∴∠ADF=∠ACG,
∵$\frac{AD}{AC}$=$\frac{DF}{CG}$,
∴△ADF∽△ACG,
∴∠DAF=∠CAF,
即∠BAG=∠CAG,AG是∠BAC的平分线,
∴$\frac{AC}{AB}=\frac{CG}{BG}$,
∴$\frac{DF}{CG}=\frac{CG}{BG}$,
∴CG2=DF•BG.
点评 本题考查了相似三角形的判定与性质以及角平分线的性质;熟练掌握相似三角形的判定与性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列根据等式的性质变形正确的是( )
| A. | 由-$\frac{1}{3}$x=y,得x=y+$\frac{1}{3}$ | B. | 由5x-2=4x+6,x=4 | ||
| C. | 由3x-5=2x,得x=5 | D. | 由x-5=7,得x=7-5 |
6.下列各组式子中,两个单项式是同类项的是( )
| A. | 2a与a2 | B. | xy2与x2y | C. | 5a2b与a2b | D. | 0.3mn2与0.3my2 |

 在平面直角坐标系中,已知点A(8,0)、B(0,6),以AB为边在第一象限内作等腰直角三角形ABC,则另一顶点C的坐标为(7,7),(14,8),(6,14).
在平面直角坐标系中,已知点A(8,0)、B(0,6),以AB为边在第一象限内作等腰直角三角形ABC,则另一顶点C的坐标为(7,7),(14,8),(6,14). △ABC中,AB=AC,三条高AD,BE,CF相交于O,那么图中全等的三角形有7对.
△ABC中,AB=AC,三条高AD,BE,CF相交于O,那么图中全等的三角形有7对.