题目内容
3.在Rt△ABC中,∠C=90°,AC=4cm,AB=5cm,△ABC的内心与顶点C的距离为( )| A. | 1cm | B. | $\sqrt{2}$cm | C. | $\sqrt{3}$cm | D. | 3cm |
分析 如图,⊙O为△ABC的内切圆,作OD⊥AC于D,OE⊥BC于E,OF⊥AB于F,设⊙O的半径为r,则OD=OE=r,先得到四边形ODCE为正方形,则CD=CE=r,根据切线长定理得到AD=AF=4-r,BE=BF=3-r,则4-r+3-r=5,解得r=1,然后根据正方形的性质求出OC即可.
解答 解: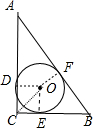 如图,⊙O为△ABC的内切圆,作OD⊥AC于D,OE⊥BC于E,OF⊥AB于F,
如图,⊙O为△ABC的内切圆,作OD⊥AC于D,OE⊥BC于E,OF⊥AB于F,
设⊙O的半径为r,则OD=OE=r,
易得四边形ODCE为正方形,
∴CD=CE=r,
∴AD=AF=4-r,BE=BF=3-r,
而AF+BF=AB,
∴4-r+3-r=5,解得r=1,
∴OC=$\sqrt{2}$OD=$\sqrt{2}$,
即△ABC的内心与顶点C的距离为$\sqrt{2}$.
故选B.
点评 本题考查了三角形内心的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了切线的性质.

练习册系列答案
相关题目
14.下列命题中的真命题是( )
| A. | 在△ABC中,∠A:∠B:∠C=3:4:5,则△ABC是锐角三角形 | |
| B. | 同位角相等 | |
| C. | 若a2=b2,则a=b | |
| D. | 有公共顶点且相等的角是对顶角 |
8.下列根据等式的性质变形正确的是( )
| A. | 由-$\frac{1}{3}$x=y,得x=y+$\frac{1}{3}$ | B. | 由5x-2=4x+6,x=4 | ||
| C. | 由3x-5=2x,得x=5 | D. | 由x-5=7,得x=7-5 |
 在平面直角坐标系中,已知点A(8,0)、B(0,6),以AB为边在第一象限内作等腰直角三角形ABC,则另一顶点C的坐标为(7,7),(14,8),(6,14).
在平面直角坐标系中,已知点A(8,0)、B(0,6),以AB为边在第一象限内作等腰直角三角形ABC,则另一顶点C的坐标为(7,7),(14,8),(6,14).