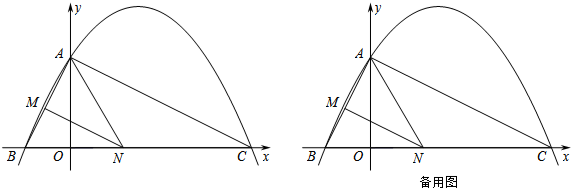题目内容
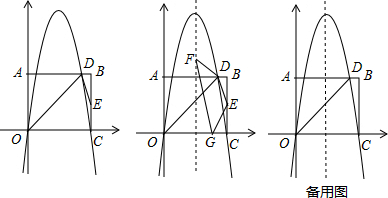
20. 如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.
如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.(1)求S关于x的函数表达式;
(2)当S取最大值时,求过点P、A、P′的二次函数表达式;
(3)在(2)中所求的二次函数图象上是否存在一点E,使△PP′E的面积为5?若存在,请求处E点坐标,若不存在,说明理由.
分析 (1)先由勾股定理求出BC=8,根据直角三角形斜边上的中线等于斜边的一半得出AD=BD=DC=$\frac{1}{2}$BC=4,再由四边形QDPP′为平行四边形,DQ=x,得到AF=PF=P′F=$\frac{1}{2}$x,那么DF=AD-AF=4-$\frac{1}{2}$x,进而可得S关于x的函数解析式;
(2)由(1)可得,其解析式为二次函数,利用配方法可得当x=4时,S取最大值,此时Q点运动到C点,P点运动到AB的中点,进而可得过点P,A,P′的二次函数解析式;
(3)首先假设存在,并设点E坐标为(x,y),表示出△PP′E的面积,可得x与y的值,判断出存在.
解答 解:(1)∵△ABC是等腰直角三角形,AB=AC=4$\sqrt{2}$,
∴BC=8,
∵D为斜边BC的中点,
∴AD=BD=DC=$\frac{1}{2}$BC=4,
∵四边形QDPP′为平行四边形,DQ=x,
∴PP′=DQ=x,
∴AF=PF=P′F=$\frac{1}{2}$x,
∴DF=AD-AF=4-$\frac{1}{2}$x,
∴S=x(4-$\frac{1}{2}$x)=-$\frac{1}{2}$x2+4x;
(2)∵S=-$\frac{1}{2}$x2+4x=-$\frac{1}{2}$(x-4)2+8,
∴当x=4时,S取最大值,此时Q点运动到C点,P点运动到AB的中点,
则点A、P、P′的坐标分别为(0,4)、(-2,2)、(2,2).
设过上述三点的二次函数解析式为y=ax2+4,
代入P′点坐标得4a+4=2,解得a=-$\frac{1}{2}$,
∴当S取最大值时,求过点P、A、P′的二次函数表达式为y=-$\frac{1}{2}$x2+4;
(3)如图,假设在y=-$\frac{1}{2}$x2+4的图象上存在一点E,使S△PP′E=5,
设E的坐标为(x,y),
则S△PP′E=$\frac{1}{2}$×PP′×|y-2|=5,即$\frac{1}{2}$×4×|y-2|=5,
解得y=$\frac{9}{2}$或y=-$\frac{1}{2}$.
当y=$\frac{9}{2}$时,-$\frac{1}{2}$x2+4=$\frac{9}{2}$,此方程无解;
当y=-$\frac{1}{2}$时,-$\frac{1}{2}$x2+4=-$\frac{1}{2}$,解得x=±3.
故在y=-$\frac{1}{2}$x2+4的图象上存在点E,使S△PP′E=5,此时E点坐标是(-3,-$\frac{1}{2}$),(3,-$\frac{1}{2}$).
点评 本题既是二次函数综合题,又是动点运动问题.考查了勾股定理,直角三角形、平行四边形的性质,待定系数法求二次函数的解析式,二次函数的性质,三角形的面积等知识,难度较大.解答第(1)问时,要“以静制动”,即图形运动到某一位置时,观察?QDPP′的底和高与自变量x的关系,得出PP′=DQ=x和DF=4-$\frac{1}{2}$x是解答此问的关键;第(3)问是“是否存在型”问题,解题策略是“假设存在,推到定论”,即假设存在符合条件的点E,根据题意得出方程,根据方程的解的情况判断点E是否存在,注意分类讨论思想的应用.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 如图,C在以AB为直径的半圆⊙O上,I是△ABC的内心,AI,BI 的延长线分别交半圆⊙O于点D,E,AB=6,则DE的长为( )
如图,C在以AB为直径的半圆⊙O上,I是△ABC的内心,AI,BI 的延长线分别交半圆⊙O于点D,E,AB=6,则DE的长为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 5 |