题目内容
4.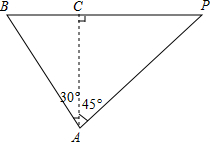 如图,一艘轮船原在A处,它的北偏东45方向上有一灯塔P,轮船沿着北偏西30方向航行4小时到达B处,这时灯塔P正好在轮船的正东方向上,已知轮船的速度为25海里/时.求轮船在B处时与灯塔P的距离(结果保留根号).
如图,一艘轮船原在A处,它的北偏东45方向上有一灯塔P,轮船沿着北偏西30方向航行4小时到达B处,这时灯塔P正好在轮船的正东方向上,已知轮船的速度为25海里/时.求轮船在B处时与灯塔P的距离(结果保留根号).
分析 可做AC⊥BP,从而构造两个直角三角形,再根据特殊角的三角函数值解答即可.
解答 解:作AC⊥BP,在Rt△ABC中,∠BAC=30°,AB=25×4=100,
∴BC=50,AC=50$\sqrt{3}$,
在Rt△ACP中,∠CAP=∠APC=45°,
∴CP=AC=50$\sqrt{3}$.
∴BP=BC+CP=50+50$\sqrt{3}$.
答:轮船在B处时与灯塔P的距离为(50+50$\sqrt{3}$)海里.
点评 本题主要考查方向角问题,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
19.近似数1.30是由数x四舍五入得到的数,则数x的取值范围是( )
| A. | 1.25≤x<1.35 | B. | 1.295≤x<1.305 | C. | 1.25<x<1.35 | D. | 1.295<x<1.305 |
14.下列结论正确的是( )
| A. | 3a2b-a2b=2 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\frac{{a}^{2}-1}{a+1}$有意义的x的取值范围是x>-1 | |
| D. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 |