题目内容
19. 屈原食品公司接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只5元.为按时完成任务,该企业招收了新工人,设新工人小明第x天生产的粽子数量为n只,n与x满足如下关系式:$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}(0<x≤5)\\(5<x≤15)\end{array}$.
屈原食品公司接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只5元.为按时完成任务,该企业招收了新工人,设新工人小明第x天生产的粽子数量为n只,n与x满足如下关系式:$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}(0<x≤5)\\(5<x≤15)\end{array}$.(1)小明第几天生产的粽子数量为390只?
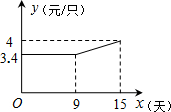
(2)设第x天每只粽子的成本是y元,y与x之间的关系的函数图象如图所示.若小明第x天的净利润为w元,试求w与x之间的函数表达式,并求出第几天的净利润最大?最大值是多少元?(提示:净利润=出厂价-成本)
分析 (1)把n=390代入n=30x+90,解方程即可求得;
(2)根据图象求得成本y与x之间的关系,然后根据:净利润=(出厂价-成本价)×销售量,结合x的范围整理即可得到W与x的关系式,再根据一次函数的增减性和二次函数的增减性解答.
解答 解:(1)∵45×5=225<390,
∴30x+90=390,
解得:x=10,
答:小明第10天生产的粽子数量为390只;
(2)由图象可知,当0≤x≤9时,y=3.4;
当9<x≤15时,设y=kx+b,
将(9,3.4)、(15,4)代入,得:$\left\{\begin{array}{l}{9k+b=3.4}\\{15k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.1}\\{b=2.5}\end{array}\right.$,
∴y=0.1x+2.5;
①当0≤x≤5时,w=(5-3.4)×45x=72x,
∵w随x的增大而增大,
∴当x=5时,w取得最大值,w最大=360元;
②当5<x≤9时,w=(5-3.4)(30x+90)=48x+144,
∵w随x的增大而增大,
∴当x=9时,w取得最大值,w最大=576元;
③当9<x≤15时,w=[5-(0.1x+2.5)](30x+90)
=-3x2+66x-225
=-3(x-11)2+138,
∴当x=11时,w取得最大值,w最大=138元;
综上,当x=9时,w取得最大值,w最大=576元,
答:第9天的净利润最大,最大值是576元.
点评 本题考查的是二次函数在实际生活中的应用,主要是利用二次函数的增减性求最值问题,利用一次函数的增减性求最值,难点在于读懂题目信息,列出相关的函数关系式.

练习册系列答案
相关题目
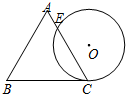 如图,一个边长为4cm的等边三角形的高与ABC与⊙O直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为3cm.
如图,一个边长为4cm的等边三角形的高与ABC与⊙O直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为3cm.