题目内容
若(2x+a)(x﹣1)的结果中不含x的一次项,则a=_____.
 2.
【解析】试题解析:(2x+a)(x-1)=2x2+(a-2)x-a,
由结果中不含x的一次项,得到a-2=0,即a=2.
2.
【解析】试题解析:(2x+a)(x-1)=2x2+(a-2)x-a,
由结果中不含x的一次项,得到a-2=0,即a=2.
练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
若□×3xy=3x2y,则□内应填的单项式是( )
A. xy B. 3xy C. x D. 3x
 C
【解析】试题分析:根据题意列出算式,计算即可得到结果.
【解析】
根据题意得:3x2y÷3xy=x,
故选:C
C
【解析】试题分析:根据题意列出算式,计算即可得到结果.
【解析】
根据题意得:3x2y÷3xy=x,
故选:C 如图,已知三角形ABC中有正方形EDFC,请你简述三角形AED到三角形PFD的变化过程是:_____________________________________
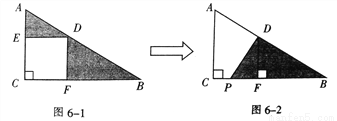
 以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD
【解析】试题分析:由图可知三角形AED到三角形PFD,点D位置不变,点A至点P,点E至点F,AD=PD,ED=FD,根据旋转的性质可知:以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD.
故答案为:以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD.
以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD
【解析】试题分析:由图可知三角形AED到三角形PFD,点D位置不变,点A至点P,点E至点F,AD=PD,ED=FD,根据旋转的性质可知:以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD.
故答案为:以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD. 计算:(-3)+4的结果等于( )
A. +7 B. -7 C. 1 D. -1
 C
【解析】试题分析:原式=+(4-3)=1.
故选C.
C
【解析】试题分析:原式=+(4-3)=1.
故选C. 观察下列运算并填空.
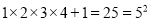 ;
;
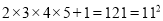 ;
;
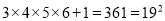 ;
; 
根据以上结果,猜想并研究: 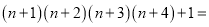 __________.
__________.
 【解析】试题解析:
…
故答案为: .
【解析】试题解析:
…
故答案为: . 小明计算一个二项式的平方时,得到正确结果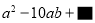 ,但最后一项不慎被污染了,这一项应
,但最后一项不慎被污染了,这一项应
是( ).
A. 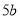 B.
B. 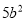 C.
C. 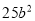 D.
D. 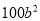
 C
【解析】试题解析:
∵?10ab=2a×(?5)×b,
∴最后一项为
故选C.
C
【解析】试题解析:
∵?10ab=2a×(?5)×b,
∴最后一项为
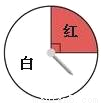
故选C. 下面是两个可以自由转动的转盘,转动转盘,分别计算转盘停止后,指针落在红色区域的概率.
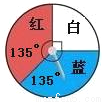
 【解析】分析:本题考察对概率意义的理解,关键是根据图示,由圆心角的度数求出概率.
本题解析:
由图可以看出,在第一个转盘内,红色区域的圆心角是90°,因此可以算得指针落在红色区域的概率是;在第二个转盘内,红色区域的圆心角是135°,因此可以算得指针落在红色区域的概率是 .
【解析】分析:本题考察对概率意义的理解,关键是根据图示,由圆心角的度数求出概率.
本题解析:
由图可以看出,在第一个转盘内,红色区域的圆心角是90°,因此可以算得指针落在红色区域的概率是;在第二个转盘内,红色区域的圆心角是135°,因此可以算得指针落在红色区域的概率是 . 从1至9这些数字中任意取一个,取出的数字是偶数的概率是( )
A. 0 B. 1 C. 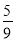 D.
D. 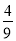
 D
【解析】在1至9这些数字中,共有2,4,6,8四个偶数,因此从这九个数字中任意取一个,取出的数字是偶数的概率是.故选D.
D
【解析】在1至9这些数字中,共有2,4,6,8四个偶数,因此从这九个数字中任意取一个,取出的数字是偶数的概率是.故选D. 如图5—13,在△ABC中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D、C、F、E,则_______是△ABC中BC边上的高,_________是△ABC中AB边上的高,_________是 △ABC中AC边上的高,CF是△ABC的高,也是△_______、△_______、△_______、△_________的高.
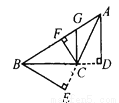
 AD CF BE BFC FGC FAC GAC
【解析】试题解析:AD是△ABC中BC边上的高,是△ABC中AB边上的高,BE是△ABC中AC边上的高,CF是△ABC的高,也是△BFC、△FGC、△FAC、△GAC的高.
故答案是:AD、CF、BE、BFC、FGC、FAC、GAC.
AD CF BE BFC FGC FAC GAC
【解析】试题解析:AD是△ABC中BC边上的高,是△ABC中AB边上的高,BE是△ABC中AC边上的高,CF是△ABC的高,也是△BFC、△FGC、△FAC、△GAC的高.
故答案是:AD、CF、BE、BFC、FGC、FAC、GAC. 
