题目内容
18.我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”,“面线”被这个平面图形截得的线段叫做该图形的“面径”(例如圆的直径就是它的“面径”).已知等边三角形的边长为4,则它的“面径”长x的取值范围是2$\sqrt{2}$≤x≤2$\sqrt{3}$.分析 根据等边三角形的性质,①最长的面径是等边三角形的高线;②最短的面径平行于三角形一边,最长的面径为等边三角形的高,然后根据相似三角形面积的比等于相似比的平方求出最短面径.
解答 解:如图,
①等边三角形的高AD是最长的面径,
AD=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$;
②当EF∥BC时,EF为最短面径,
此时,($\frac{EF}{BC}$)2=$\frac{1}{2}$,
即$\frac{EF}{4}$=$\frac{\sqrt{2}}{2}$,
解得EF=2$\sqrt{2}$.
所以,它的面径长2$\sqrt{2}$≤x≤2$\sqrt{3}$
故答案为:2$\sqrt{2}$≤x≤2$\sqrt{3}$.
点评 本题考查了等边三角形的性质,读懂题意,弄明白面径的定义,并准确判断出等边三角形的最短与最长的面径是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
3.抛物线y=-x2+2kx+2与x轴的交点个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
7.下列计算结果正确的是( )
| A. | a3+a3=a6 | B. | x2•x3=x6 | C. | (-a)2÷2a=2a | D. | (-2xy2)3=-8x3y6 |
8.下列计算正确的是( )
| A. | $(-\frac{1}{2})^{2}=-\frac{1}{4}$ | B. | 3a-2=$\frac{1}{3{a}^{2}}$ | C. | (-1)0=1 | D. | 00=1 |
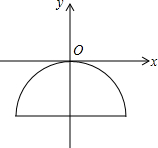 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米. 如图,在平面直角坐标系中,直线y=kx+5与x轴交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.
如图,在平面直角坐标系中,直线y=kx+5与x轴交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.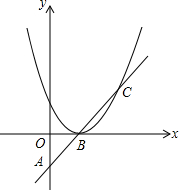 如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.
如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.