题目内容
14.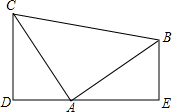 如图,已知AB⊥AC,AB=AC,DE过点A,且CD⊥DE,BE⊥DE,垂足分别为点D,E.求证:△ADC≌△BEA.
如图,已知AB⊥AC,AB=AC,DE过点A,且CD⊥DE,BE⊥DE,垂足分别为点D,E.求证:△ADC≌△BEA.
分析 由AB与AC垂直,CD与DE垂直,B与DE垂直,利用同角的余角相等得出∠DCA=∠EAB,进而得出的一对角相等,一对直角相等,以及AB=AC,利用AAS即可得证.
解答 证明:∵AB⊥AC,CD⊥DE,BE⊥DE,
∴∠BAC=∠D=∠E=90°,
∴∠CAD+∠BAE=90°,∠DCA+∠CAD=90°,
∴∠DCA=∠EAB;
在△ADC和△BEA中,
$\left\{\begin{array}{l}{∠D=∠E=90°}\\{∠DCA=∠EAB}\\{AC=BA}\end{array}\right.$,
∴△ADC≌△BEA(AAS).
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
4.下列命题的逆命题是真命题的是( )
| A. | 若a的倒数为$\frac{1}{a}$,则a是整数 | |
| B. | 若三个数满足a2+b2=c2,则a、b、c一定是三角形的三条边 | |
| C. | 若△ABC与△A'B'C'关于某直线对称,则△ABC与△A'B'C'一定全等 | |
| D. | 两直线平行,同旁内角互补 |
5.下列计算错误的是( )
| A. | 3$\sqrt{3}$-$\sqrt{3}$=2$\sqrt{3}$ | B. | a0=1 | C. | -2+|-2|=0 | D. | (-3)-2=$\frac{1}{9}$ |
19.将抛物线y=(x-1)2+2向右平移3个单位长度,再向上平移2个单位长度后,得到的抛物线的解析式为( )
| A. | y=(x-4)2+4 | B. | y=(x-4)2+6 | C. | y=(x+2)2+6 | D. | y=(x-1)2+4 |
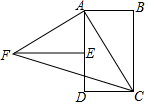 如图四边形ABCD为长方形,△ABC旋转后能与△AEF重合
如图四边形ABCD为长方形,△ABC旋转后能与△AEF重合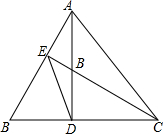 如图,△ABC中,∠B=60°,AD⊥BC,CE⊥AB,说明:
如图,△ABC中,∠B=60°,AD⊥BC,CE⊥AB,说明: