题目内容
4.一个不透明的口袋中有3个小球,上面分别标有数字2,3,4,每个小球除数字不同外其他都相同,小颖先从口袋中随机摸出个小球,记下数字后放回并搅匀;再从口袋中随机摸出一个小球,用画树状图(或列表)的方法,求小颖两次摸出的小球上的数字之和为6的概率.分析 利用列表法展示所有9种等可能的结果数,再找出两次摸出小球上的数字之和为6的结果数,然后根据概率公式求解.
解答 解:列表如下:
| 2 | 3 | 4 | |
| 2 | 4 | 5 | 6 |
| 3 | 5 | 6 | 7 |
| 4 | 6 | 7 | 8 |
∴小颖两次摸出的小球上的数字之和为6的概率$\frac{3}{9}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
9.如果a,b互为相反数,那么(6a2-12a)-6(a2+2b-5)的值为( )
| A. | -18 | B. | 18 | C. | 30 | D. | -30 |
13.若x=3是关于x的方程4x-(2a+1)=3x+3a-1的解,则a的值为( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{5}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
14.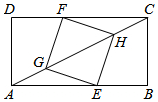 如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
 如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | $\frac{9}{2}$ | D. | $\frac{25}{4}$ |
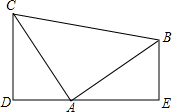 如图,已知AB⊥AC,AB=AC,DE过点A,且CD⊥DE,BE⊥DE,垂足分别为点D,E.求证:△ADC≌△BEA.
如图,已知AB⊥AC,AB=AC,DE过点A,且CD⊥DE,BE⊥DE,垂足分别为点D,E.求证:△ADC≌△BEA.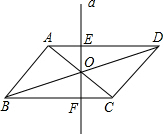 在?ABCD中,对角线AC、BD相交于点O,直线a经过点O,且与边AD、BC交于点E、F,线段OE和OF有怎样的数量关系?为什么?
在?ABCD中,对角线AC、BD相交于点O,直线a经过点O,且与边AD、BC交于点E、F,线段OE和OF有怎样的数量关系?为什么?