题目内容
如图,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究在第n个图中,黑、白瓷砖分别各有多少块( )


| A、4n+6,n(n+1) |
| B、4n+6,n(n+2) |
| C、n(n+1),4n+6 |
| D、n(n+2),4n+6 |
考点:规律型:图形的变化类
专题:
分析:分别清点题目给出的三个图形中的白瓷砖和黑瓷砖的块数,然后通过分析,找出白瓷砖和黑瓷砖的块数与图形数之间的规律,即可解答此题.
解答:解:通过观察图形可知,当n=1时,用白瓷砖2块,黑瓷砖10块;
当n=2时,用白瓷砖6块,黑瓷砖14块;
当n=3时,用白瓷砖12块,黑瓷砖18块;
可以发现,需要白瓷砖的数量和图形数之间存在这样的关系,即白瓷砖块数等于图形数的平方加上图形数;
需要黑瓷砖的数量和图形数之间存在这样的关系,即黑瓷砖块数等于图形数的4倍加上图形数.
所以,在第n个图形中,白瓷砖的块数可用含n的代数式表示为n(n+1);
白瓷砖的块数可用含n的代数式表示为4n+6.
故选:C.
当n=2时,用白瓷砖6块,黑瓷砖14块;
当n=3时,用白瓷砖12块,黑瓷砖18块;
可以发现,需要白瓷砖的数量和图形数之间存在这样的关系,即白瓷砖块数等于图形数的平方加上图形数;
需要黑瓷砖的数量和图形数之间存在这样的关系,即黑瓷砖块数等于图形数的4倍加上图形数.
所以,在第n个图形中,白瓷砖的块数可用含n的代数式表示为n(n+1);
白瓷砖的块数可用含n的代数式表示为4n+6.
故选:C.
点评:此题主要考查学生对图形变化的规律,解答此题的关键是通过观察和分析,找出其中的规律,利用规律解决问题.

练习册系列答案
相关题目
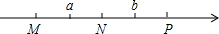 如图,M,N,P分别是数轴上三个整数对应的点,且MN=NP=1,数a对应的点在M与N之间,数b对应的点在N和P之间,若|a|+|b|=2,则在M、N、P三个点中,原点不可能是( )
如图,M,N,P分别是数轴上三个整数对应的点,且MN=NP=1,数a对应的点在M与N之间,数b对应的点在N和P之间,若|a|+|b|=2,则在M、N、P三个点中,原点不可能是( )| A、M | B、N | C、P | D、M或P |
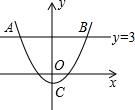 如图,抛物线y=ax2+c与直线y=3相交于A、B,点A的横坐标为-4,与y轴相交于点C(0,-1),从图象可知,当0≤ax2+c≤3时,自变量x的取值范围是( )
如图,抛物线y=ax2+c与直线y=3相交于A、B,点A的横坐标为-4,与y轴相交于点C(0,-1),从图象可知,当0≤ax2+c≤3时,自变量x的取值范围是( )| A、-4≤x≤3 |
| B、-4≤x≤-2或2≤x≤4 |
| C、-4≤x≤4 |
| D、x≤-2或x≥2 |
 已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到,这时图象与x轴的交点为A、B(A在B的左边),与y轴交于点C.
已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到,这时图象与x轴的交点为A、B(A在B的左边),与y轴交于点C.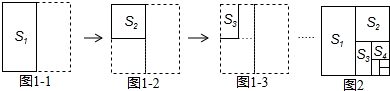
 如图,直线AB,CD,EF相交于点O,∠AOF=120°,∠BOD=90°,求∠BOF,∠EOC的度数.
如图,直线AB,CD,EF相交于点O,∠AOF=120°,∠BOD=90°,求∠BOF,∠EOC的度数.