题目内容
 如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=
如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB,AC于F,E,以下结论:①MB⊥BD,②FD=EC,③EC=EF+DG,④CE=| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:等腰三角形的判定与性质
专题:
分析:如图,由BD分别是∠ABC及其外角的平分线,得到∠MBD=
×180°=90°,故①成立;证明BF=CE、BF=DF,得到FD=CE,故②成立;证明BF为直角△BDM的斜边上的中线,故④成立.
| 1 |
| 2 |
解答: 解:如图,∵BD分别是∠ABC及其外角的平分线,
解:如图,∵BD分别是∠ABC及其外角的平分线,
∴∠MBD=
×180°=90°,
故MB⊥BD,①成立;
∵DM∥BC,
∴
=
,而AB=AC,
∴BF=CE;
∵DF∥BC,
∴∠FDB=∠DBC;
∵∠FBD=∠DBC,
∴∠FBD=∠FDB,
∴FD=BF,FD=EC,②成立;
∵∠DBM=90°,MF=DF,
∴BF=
DM,而CE=BF,
∴CE=
DM,④成立.
故选C.
 解:如图,∵BD分别是∠ABC及其外角的平分线,
解:如图,∵BD分别是∠ABC及其外角的平分线,∴∠MBD=
| 1 |
| 2 |
故MB⊥BD,①成立;
∵DM∥BC,
∴
| AB |
| BF |
| AC |
| CE |
∴BF=CE;
∵DF∥BC,
∴∠FDB=∠DBC;
∵∠FBD=∠DBC,
∴∠FBD=∠FDB,
∴FD=BF,FD=EC,②成立;
∵∠DBM=90°,MF=DF,
∴BF=
| 1 |
| 2 |
∴CE=
| 1 |
| 2 |
故选C.
点评:该题主要考查了等腰三角形的判定及其性质、直角三角形的性质等几何知识点及其应用问题;应牢固掌握等腰三角形的判定及其性质、直角三角形的性质.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
小明的爸爸买了利率为3.96%的3年期债券,到期后可获得本息1678元,则小明的爸爸买债券花了( )
| A、1500元 |
| B、1600元 |
| C、1700元 |
| D、1800元 |
 如图,OP是∠AOB的平分线,则下列说法错误的是( )
如图,OP是∠AOB的平分线,则下列说法错误的是( )| A、∠AOB=2∠AOP | ||
B、∠AOP=
| ||
C、∠AOB=
| ||
| D、∠AOP=∠BOP |
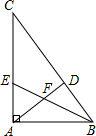 在△ABC中,∠CAB=90°,AD⊥BC于D,BE平分∠CBA交AC于E,交AD于F,求证:AE=AF.
在△ABC中,∠CAB=90°,AD⊥BC于D,BE平分∠CBA交AC于E,交AD于F,求证:AE=AF. 在三角形ABC中,AD是中线,GD=
在三角形ABC中,AD是中线,GD= 某船在大海上行到O处,沿北偏东60°方向航行2海里后,再沿北偏西30°方向航行2海里,以下面线段AB为一海里,在下图上画同航线.
某船在大海上行到O处,沿北偏东60°方向航行2海里后,再沿北偏西30°方向航行2海里,以下面线段AB为一海里,在下图上画同航线.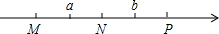 如图,M,N,P分别是数轴上三个整数对应的点,且MN=NP=1,数a对应的点在M与N之间,数b对应的点在N和P之间,若|a|+|b|=2,则在M、N、P三个点中,原点不可能是( )
如图,M,N,P分别是数轴上三个整数对应的点,且MN=NP=1,数a对应的点在M与N之间,数b对应的点在N和P之间,若|a|+|b|=2,则在M、N、P三个点中,原点不可能是( )