题目内容
20. 某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:$\sqrt{3}$.
某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:$\sqrt{3}$.(1)求新坡面的坡角a;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
分析 (1)由新坡面的坡度为1:$\sqrt{3}$,可得tanα=tan∠CAB=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,然后由特殊角的三角函数值,求得答案;
(2)首先过点C作CD⊥AB于点D,由坡面BC的坡度为1:1,新坡面的坡度为1:$\sqrt{3}$.即可求得AD,BD的长,继而求得AB的长,则可求得答案.
解答 解:(1)∵新坡面的坡度为1:$\sqrt{3}$,
∴tanα=tan∠CAB=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠α=30°.
答:新坡面的坡角a为30°;
(2)文化墙PM不需要拆除. 过点C作CD⊥AB于点D,则CD=6,
过点C作CD⊥AB于点D,则CD=6,
∵坡面BC的坡度为1:1,新坡面的坡度为1:$\sqrt{3}$,
∴BD=CD=6,AD=6$\sqrt{3}$,
∴AB=AD-BD=6$\sqrt{3}$-6<8,
∴文化墙PM不需要拆除.
点评 此题考查了坡度坡角的知识.注意根据题意构造直角三角形是关键.

练习册系列答案
相关题目
13.如图,图(1)是一枚古代钱币,图(2)是类似图(1)的几何图形,将图(2)中的图形沿一条对称轴折叠得到图(3),关于图(3)描述正确的是( )


| A. | 只是轴对称图形 | |
| B. | 只是中心对称图形 | |
| C. | 既是轴对称图形又是中心对称图形 | |
| D. | 既不是轴对称图形也不是中心对称图形 |

 数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,求AF的长.
数学拓展课程《玩转学具》课堂中,小陆同学发现:一副三角板中,含45°的三角板的斜边与含30°的三角板的长直角边相等,于是,小陆同学提出一个问题:如图,将一副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,求AF的长.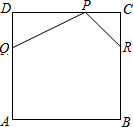 如图,正方形ABCD是一张边长为12公分的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P、Q、
如图,正方形ABCD是一张边长为12公分的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P、Q、 如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.
如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB. 如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D=48°.
如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D=48°.


