题目内容
5．
如图，点A，B，C，D在同一条直线上，CE∥DF，EC=BD，AC=FD．求证：AE=FB．
分析 根据CE∥DF，可得∠ACE=∠D，再利用SAS证明△ACE≌△FDB，得出对应边相等即可．
解答 证明：∵CE∥DF，
∴∠ACE=∠D，
在△ACE和△FDB中，
$\left\{\begin{array}{l}{AC=FD}&{\;}\\{∠ACE=∠D}&{\;}\\{EC=BD}&{\;}\end{array}\right.$，
∴△ACE≌△FDB（SAS），
∴AE=FB．
点评 此题主要考查全等三角形的判定与性质和平行线的性质；熟练掌握平行线的性质，证明三角形全等是解决问题的关键．
练习册系列答案
相关题目
16．分别取正整数5的绝对值、倒数、相反数、算术平方根，得到的数值仍为正整数的是（ ）
| A． | 绝对值 | B． | 倒数 | C． | 相反数 | D． | 算术平方根 |
13．
如图的矩形ABCD中，E点在CD上，且AE＜AC．若P、Q两点分别在AD、AE上，AP：PD=4：1，AQ：QE=4：1，直线PQ交AC于R点，且Q、R两点到CD的距离分别为q、r，则下列关系何者正确？（ ）
如图的矩形ABCD中，E点在CD上，且AE＜AC．若P、Q两点分别在AD、AE上，AP：PD=4：1，AQ：QE=4：1，直线PQ交AC于R点，且Q、R两点到CD的距离分别为q、r，则下列关系何者正确？（ ）| A． | q＜r，QE=RC | B． | q＜r，QE＜RC | C． | q=r，QE=RC | D． | q=r，QE＜RC |
某地的一座人行天桥如图所示，天桥高为6米，坡面BC的坡度为1：1，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为1：$\sqrt{3}$．
10．
如图，在5×5的正方形网格中，从在格点上的点A，B，C，D中任取三点，所构成的三角形恰好是直角三角形的概率为（ ）
如图，在5×5的正方形网格中，从在格点上的点A，B，C，D中任取三点，所构成的三角形恰好是直角三角形的概率为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
17．在$\sqrt{2}$，-1，-3，0这四个实数中，最小的是（ ）
| A． | $\sqrt{2}$ | B． | -1 | C． | -3 | D． | 0 |
13．
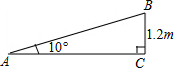一个公共房门前的台阶高出地面1.2米，台阶拆除后，换成供轮椅行走的斜坡，数据如图所示，则下列关系或说法正确的是（ ）
一个公共房门前的台阶高出地面1.2米，台阶拆除后，换成供轮椅行走的斜坡，数据如图所示，则下列关系或说法正确的是（ ）| A． | 斜坡AB的坡度是10° | B． | 斜坡AB的坡度是tan10° | ||
| C． | AC=1.2tan10°米 | D． | AB=$\frac{1.2}{cos10°}$米 |