题目内容
16.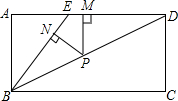 如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.
如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.(1)求证:BE=DE;
(2)试判断AB和PM,PN的数量关系并说明理由.
分析 (1)由矩形的性质得出∠ADB=∠CBD,由已知条件∠CBD=∠EBD,证出∠ADB=∠EBD,即可得出结论;(2)延长MP交BC于Q,先由角的平分线性质得出PQ=PN,再由AB=MQ,即可得出结论.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵∠CBD=∠EBD,
∴∠ADB=∠EBD,
∴BE=DE;
(2)解:PM+PN=AB;理由如下:
延长MP交BC于Q,如图所示: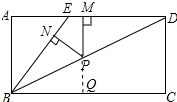 ∵AD∥BC,PM⊥AD,
∵AD∥BC,PM⊥AD,
∴PQ⊥BC,
∵∠CBD=∠EBD,PN⊥BE,
∴PQ=PN,
∴AB=MQ=PM+PQ=PM+PN.
点评 本题考查了矩形的性质、平行线的性质以及角平分线的性质;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
4.下列几何体的主视图、左视图、俯视图都相同的是( )
| A. |  | B. |  | C. |  | D. |  |
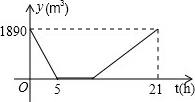 某游泳池内现存水1890立方米,已知该游泳池的防水速度是进水速度的2倍,假设在换水时需要经历“放水→清洗→进水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.试根据图象解答下列问题:
某游泳池内现存水1890立方米,已知该游泳池的防水速度是进水速度的2倍,假设在换水时需要经历“放水→清洗→进水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.试根据图象解答下列问题: