题目内容
11．若二次函数y=2x2-x-m与x轴有两个交点，则m的取值范围是m＞-$\frac{1}{8}$．分析 抛物线与x轴有两个交点，则△=b2-4ac＞0，从而求出m的取值范围．
解答 解：∵二次函数y=2x2-x-m与x轴有两个交点，
∴△=1-4×2（-m）＞0，
∴m＞-$\frac{1}{8}$，
故答案为m＞-$\frac{1}{8}$．
点评 本题考查了抛物线与x轴的交点问题，需要掌握：①抛物线与x轴有两个交点，则△＞0；②抛物线与x轴无交点，则△＜0；③抛物线与x轴有一个交点，则△=0．
练习册系列答案
相关题目
如图，在锐角三角形ABC中，AD⊥BC于D，E、F、G分别是AC、AB、BC的中点．求证：FG=DE．
2．
甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步，先到终点的人原地休息．已知甲先出发3秒，在跑步过程中，甲、乙两人的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，则下列结论正确的是（ ）
甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步，先到终点的人原地休息．已知甲先出发3秒，在跑步过程中，甲、乙两人的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，则下列结论正确的是（ ）| A． | 乙的速度是4米/秒 | |
| B． | 离开起点后，甲、乙两人第一次相遇时，距离起点12米 | |
| C． | 甲从起点到终点共用时83秒 | |
| D． | 乙到达终点时，甲、乙两人相距68米 |
19．
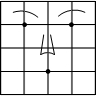如图中的一张脸，小明说：“如果我用（0，2）表示左眼，用（2，2）表示右眼”，那么嘴的位置可以表示成（ ）
如图中的一张脸，小明说：“如果我用（0，2）表示左眼，用（2，2）表示右眼”，那么嘴的位置可以表示成（ ）| A． | （0，1） | B． | （2，1） | C． | （1，0） | D． | （1，-1） |
6．已知2a=3b（b≠0），则下列比例式成立的是（ ）
| A． | $\frac{a}{2}$=$\frac{b}{3}$ | B． | $\frac{a}{3}$=$\frac{b}{2}$ | C． | $\frac{a}{b}$=$\frac{2}{3}$ | D． | $\frac{a}{2}$=$\frac{3}{b}$ |
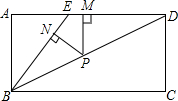如图，四边形ABCD是矩形，E为AD上一点，且∠CBD=∠EBD，P为对角线BD上一点，PN⊥BE于点N，PM⊥AD于点M．
20．等腰三角形的两条边长分别为1cm、2cm，则这个三角形的周长为（ ）
| A． | 4cm | B． | 4或5cm | C． | 5cm | D． | 3cm |