题目内容
1.不等式组$\left\{\begin{array}{l}{x+1>0}\\{x>2x-3}\end{array}\right.$的解是-1<x<3.分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{x+1>0①}\\{x>2x-3②}\end{array}\right.$
∵解不等式①得:x>-1,
解不等式②得:x<3,
∴不等式组的解集为-1<x<3,
故答案为:-1<x<3.
点评 本题考查了解一元一次不等式组的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
相关题目
11.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (-2x)3=-2x3 | ||
| C. | $\sqrt{2}+\sqrt{8}=3\sqrt{2}$ | D. | (a-b)(-a+b)=-a2-2ab-b2 |
9. 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )
 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )| A. | (-2,4) | B. | (-4,1) | C. | (-3,2) | D. | (-2,1) |
11.代数式$\frac{a}{|a|}+\frac{|b|}{b}+\frac{ab}{|ab|}$的所有不同的值有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 无数个 |
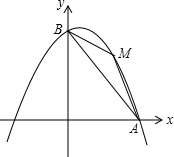 如图,抛物线y=a(x-1)2+b经过A(4,0)和B(0,4)两点.
如图,抛物线y=a(x-1)2+b经过A(4,0)和B(0,4)两点.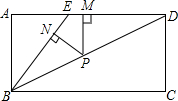 如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.
如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.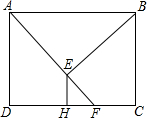 如图,矩形ABCD中,F为CD边上一点,AF=AB,BE⊥AF,EH⊥CD垂足分别为点E、H.
如图,矩形ABCD中,F为CD边上一点,AF=AB,BE⊥AF,EH⊥CD垂足分别为点E、H.