题目内容
6.在直角坐标系中,点A、B的坐标分别为(-2,4)、(-5,2),点M在x轴上,点N在y轴上,如果以点A、B、M、N为顶点的四边形是平行四边形,那么符合条件的点M有3个.分析 利用一组对边相等且平行的四边形是平行四边形进而得出答案.
解答  解:如图所示:当AB$\stackrel{∥}{=}$NM时,四边形ABMN是平行四边形,
解:如图所示:当AB$\stackrel{∥}{=}$NM时,四边形ABMN是平行四边形,
当AB$\stackrel{∥}{=}$N′M′时,四边形ABN′M′是平行四边形.
当AM$\stackrel{∥}{=}$BN时,四边形BM′AN′是平行四边形.
故符合题意的有3个点.
故答案为:3.
点评 此题考查了平行四边形的判定,结合AB的长分别确定M,N的位置是解决问题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
14.在函数y=$\sqrt{x-3}$中,自变量x的取值范围是( )
| A. | x≥3 | B. | x>3 | C. | x≤3 | D. | x<3 |
11.代数式$\frac{a}{|a|}+\frac{|b|}{b}+\frac{ab}{|ab|}$的所有不同的值有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 无数个 |
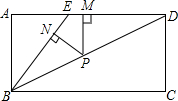 如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.
如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M. 某研究性学习小组,为了测量某池塘边A、B两点间的距离,让一架航模在直线AB的正上方24米的高度飞行,当航模位于点D处时,在A点处测得航模仰角为60°,5分钟后,当航模在点C处时,在B点测得航模仰角为45°,己知航模飞行的速度为每分钟45米,试计算A、B两点的距离.(结果精确到0.1米,参考数据:$\sqrt{2}=1.41,\sqrt{3}$=1.73.)
某研究性学习小组,为了测量某池塘边A、B两点间的距离,让一架航模在直线AB的正上方24米的高度飞行,当航模位于点D处时,在A点处测得航模仰角为60°,5分钟后,当航模在点C处时,在B点测得航模仰角为45°,己知航模飞行的速度为每分钟45米,试计算A、B两点的距离.(结果精确到0.1米,参考数据:$\sqrt{2}=1.41,\sqrt{3}$=1.73.)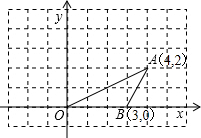 如图,点O、A、B的坐标分别为(0,0)、(4,2)、(3,0),将△OAB绕点O按逆时针方向旋转90°后,得到△OCD.(点A转到点C)
如图,点O、A、B的坐标分别为(0,0)、(4,2)、(3,0),将△OAB绕点O按逆时针方向旋转90°后,得到△OCD.(点A转到点C)