题目内容
17.如图1,在△ABC中,∠ACB=90°,点D、点E分别在AC、AB边上,连结DE、DB,使得∠DEA=90°,若点O是线段BD的中点,连结OC、OE,则易得OC=OE;操作:现将△ADE绕A点逆时针旋转得到△AFG(点D、点E分别与点F、点G对应),连结FB,若点O是线段FB的中点,连结OC、OG,探究线段OC、OG之间的数量关系;
(1)如图2,当点G在线段CA的延长线上时,OC=OG是否成立;若成立,请证明;若不成立,请说明理由;
(2)如图3,当点G在线段CA上时,线段OC=OG是否成立;若成立,请证明;若不成立,请说明理由;
(3)如图4,在△ADE的旋转过程中,线段OC、OG之间的数量关系是否发生了变化?请直接写出结论,不用说明理由.

分析 (1)先作出辅助线,再判断△BOC≌△FOD,最后用直角三角形的斜边上的中线等于斜边的一半即可;
(2)先作出辅助线,再判断△BOC≌△FOD,最后用直角三角形的斜边上的中线等于斜边的一半即可;
(3)先作出辅助线,进而判断△BOC≌△FOD,再判断出∠CAG=∠BMG,进而得出△GAC∽△GFD判断出∠CGD=90°,最后用直角三角形的斜边上的中线等于斜边的一半即可.
解答 解:(1)当点G在线段CA的延长线上时,OC=OG成立
理由:如图2,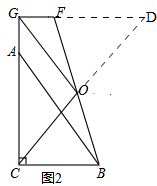
延长GF,CO相较于点D,
∵∠ACB=∠FGA=90°,
∴GD∥BC,
∴∠BCO=∠D,
∵点O是线段BD的中点,
∴OB=OF,
在△BOC和△FOD中,$\left\{\begin{array}{l}{∠BCO=∠D}\\{∠BOC=∠FOD}\\{OB=OF}\end{array}\right.$,
∴△BOC≌△FOD,
∴OC=OD,
在Rt△CDG中,OG=$\frac{1}{2}$CD=OC,
(2)当点G在线段CA上时,线段OC=OG是成立,
理由:如图3,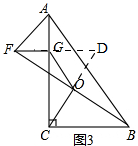
延长GF,CO相较于点D,
∵∠ACB=∠FGA=90°,
∴GD∥BC,
∴∠BCO=∠D,
∵点O是线段BD的中点,
∴OB=OF,
在△BOC和△FOD中,$\left\{\begin{array}{l}{∠BCO=∠D}\\{∠BOC=∠FOD}\\{OB=OF}\end{array}\right.$,
∴△BOC≌△FOD,
∴OC=OD,
在Rt△CDG中,OG=$\frac{1}{2}$CD=OC,
(3)在△ADE的旋转过程中,线段OC、OG之间的数量关系不发生了变化,
理由:如图4,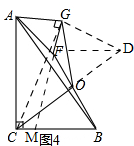
连接CG,延长GF交BC于M,过点F作FD∥BC,连接DG,
∴∠BCO=∠FDO,
∵点O是线段BD的中点,
∴OB=OF,
在△BOC和△FOD中,$\left\{\begin{array}{l}{∠BCO=∠D}\\{∠BOC=∠FOD}\\{OB=OF}\end{array}\right.$,
∴△BOC≌△FOD,
∴OC=OD,BC=DF
由题意知,△AFG∽△ABC,
∴$\frac{AF}{AB}=\frac{FG}{BC}$,
∴$\frac{AF}{AB}=\frac{FG}{DF}$,
∵∠ACB=∠AGF=90°,
∴点A,C,M,G四点共圆,
∴∠CAG=∠BMG,
∵FD∥BC,
∴∠GFD=∠BMG,
∴∠CAG=∠GFD,
∵$\frac{AF}{AB}=\frac{FG}{DF}$,
∴△GAC∽△GFD,
∴∠AGC=∠FGD,
∴∠CGD=∠ACF=90°,
∵OC=OD,
∴OG=$\frac{1}{2}$CD=OC.
点评 此题是几何变换综合题,主要考查了全等三角形的性质和判定,相似三角形的性质和判定,直角三角形的性质,解本题的关键是判断出△BOC≌△FOD,难点是(3)中判断出∠CGD=90°.

| A. | $\frac{9}{2}$,$\frac{27}{4}$ | B. | 2,$\frac{9}{2}$ | C. | $\frac{4}{3}$,2 | D. | 6,10 |
 如图,甲、乙、丙、丁四名同学有以下说法.甲说:“直线BC不过点A”;乙说:”点A在直线CD外“;丙说:”点D在线段BC的延长线上“;丁说:”射线AD与射线CD不相交“.其中正确的有( )
如图,甲、乙、丙、丁四名同学有以下说法.甲说:“直线BC不过点A”;乙说:”点A在直线CD外“;丙说:”点D在线段BC的延长线上“;丁说:”射线AD与射线CD不相交“.其中正确的有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
| A. | x(30-2x)平方厘米 | B. | x(30-x)平方厘米 | C. | x(15-x)平方厘米 | D. | x(15+x) 平方厘米 |
| A. | $\frac{1}{2}$x(x+1)=4×14 | B. | $\frac{1}{2}$x(x-1)=4×14 | C. | x(x+1)=4×14 | D. | x(x-1)=4×14 |
| A. | x$≥-\frac{1}{3}$ | B. | x$>-\frac{1}{3}$且x≠1 | C. | x$≥-\frac{1}{3}$且x≠1 | D. | -$\frac{1}{3}$≤x≤1 |
| A. | ($\frac{s}{10}$+2)h | B. | ($\frac{s}{10+2}$)h | C. | ($\frac{s}{10}$-2)h | D. | ($\frac{s}{10-2}$)h |
 如图,在Rt△ABC中,∠C=90°,BC=3,AC=6,点D是AC边上的动点,且点D从点C向点A运动.若设CD=x,△ABD的面积为y,则y与x之间的关系式为y=-$\frac{3}{2}$x+9.
如图,在Rt△ABC中,∠C=90°,BC=3,AC=6,点D是AC边上的动点,且点D从点C向点A运动.若设CD=x,△ABD的面积为y,则y与x之间的关系式为y=-$\frac{3}{2}$x+9.