题目内容
求
+
的最小值.(用两种方法解答)
| (x2+2x+2) |
| (x-2)2+162 |
考点:无理函数的最值
专题:
分析:先化简式子
+
=
+
,利用函数的几何意义是x轴上的点(x,0)与点(-1,1),(2,4)距离之和求解即可.方法一运用(-1,1)关于x轴的对称点是(-1,-1)最小值即是(-1,-1)与(2,4)之间的距离求解,方法二(-1,1)关于x轴的对称点是(-1,-1),求出过(-1,-1)与(2,4)的直线,再求出直线与x轴的交点,利用最小值即是(-
,0)与(-1,1)的距离加上(-
,0)与(2,4)的距离求解即可.
| (x2+2x+2) |
| (x-2)2+162 |
| (x+1)2+(0-1)2 |
| (x-2)2+(0-4)2 |
| 2 |
| 5 |
| 2 |
| 5 |
解答:解:方法一:
+
=
+
=
+
,
函数的几何意义是x轴上的点(x,0)与点(-1,1),(2,4)距离之和,由图象可知,(-1,1)关于x轴的对称点是(-1,-1)最小值即是(-1,-1)与(2,4)之间的距离
=
.
方法二:
+
=
+
=
+
,
函数的几何意义是x轴上的点(x,0)与点(-1,1),(2,4)距离之和,由图象可知,(-1,1)关于x轴的对称点是(-1,-1),设过(-1,-1)与(2,4)的直线为y=kx+b,
代入得
,解得
,所以直线为y=
x+
,交x轴于(-
,0),最小值即是(-
,0)与(-1,1)的距离加上(-
,0)与(2,4)的距离:
+
=
.
| (x2+2x+2) |
| (x-2)2+162 |
| (x+1)2+1 |
| (x-2)2+16 |
| (x+1)2+(0-1)2 |
| (x-2)2+(0-4)2 |
函数的几何意义是x轴上的点(x,0)与点(-1,1),(2,4)距离之和,由图象可知,(-1,1)关于x轴的对称点是(-1,-1)最小值即是(-1,-1)与(2,4)之间的距离
| (-1-2)2+(-1-4)2 |
| 34 |
方法二:
| (x2+2x+2) |
| (x-2)2+162 |
| (x+1)2+1 |
| (x-2)2+16 |
| (x+1)2+(0-1)2 |
| (x-2)2+(0-4)2 |
函数的几何意义是x轴上的点(x,0)与点(-1,1),(2,4)距离之和,由图象可知,(-1,1)关于x轴的对称点是(-1,-1),设过(-1,-1)与(2,4)的直线为y=kx+b,
代入得
|
|
| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
(-1+
|
(2+
|
| 34 |
点评:本题主要考查了无理函数的最值,解题的关键是能理清函数的几何意义.

练习册系列答案
相关题目
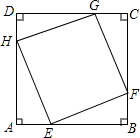 如图,点E、F、G、H分别在正方形ABCD的四条边上,并且四边形EFGH也是正方形,AB=4.
如图,点E、F、G、H分别在正方形ABCD的四条边上,并且四边形EFGH也是正方形,AB=4. 如图,在△ABC,高线BE、AD相交于点O,∠BAE=45°.
如图,在△ABC,高线BE、AD相交于点O,∠BAE=45°.