题目内容
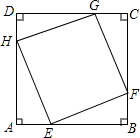 如图,点E、F、G、H分别在正方形ABCD的四条边上,并且四边形EFGH也是正方形,AB=4.
如图,点E、F、G、H分别在正方形ABCD的四条边上,并且四边形EFGH也是正方形,AB=4.(1)AE长为多少时,正方形EFGH的面积最小,最小面积是多少?
(2)若AB=a呢?AE长为多少时,正方形EFGH的面积最小,最小面积是多少?
考点:正方形的性质,二次函数的最值,全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质可得EH=HG,再根据同角的余角相等求出∠AHE=∠DGH,然后利用“角角边”证明△AHE和△DGH全等,根据全等三角形对应边相等可得DH=AE,然后表示出AH,再利用勾股定理列式求出EH2,即为正方形EFGH的面积,再利用二次函数的最值问题解答;
(2)将AB=4换成a,然后与(1)的求解方法相同.
(2)将AB=4换成a,然后与(1)的求解方法相同.
解答:解:(1)∵四边形EFGH是正方形,
∴EH=GH,
∵∠AHE+∠DHG=∠DGH+∠DHG,
∴∠AHE=∠DGH,
在△AHE和△DGH中,
,
∴△AHE≌△DGH(AAS),
∴DH=AE,
设AE=x,
∵正方形ABCD的边长AB=4,
∴AH=4-x,
由勾股定理列式求出EH2=AE2+AH2=x2+(4-x)2=2x2-8x+16=2(x-2)2+8,
即正方形EFGH的面积=2(x-2)2+8,
所以,当x=2,即AE=2时,正方形EFGH的面积最小,最小面积是8;
(2)由(1)可知,正方形EFGH的面积=x2+(a-x)2=2x2-2ax+a2=2(x-
a)2+
a2,
所以,当x=
a,即AE=
a时,正方形EFGH的面积最小,最小面积是
a2.
∴EH=GH,
∵∠AHE+∠DHG=∠DGH+∠DHG,
∴∠AHE=∠DGH,
在△AHE和△DGH中,
|
∴△AHE≌△DGH(AAS),
∴DH=AE,
设AE=x,
∵正方形ABCD的边长AB=4,
∴AH=4-x,
由勾股定理列式求出EH2=AE2+AH2=x2+(4-x)2=2x2-8x+16=2(x-2)2+8,
即正方形EFGH的面积=2(x-2)2+8,
所以,当x=2,即AE=2时,正方形EFGH的面积最小,最小面积是8;
(2)由(1)可知,正方形EFGH的面积=x2+(a-x)2=2x2-2ax+a2=2(x-
| 1 |
| 2 |
| 1 |
| 2 |
所以,当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,二次函数的最值问题,熟练掌握各性质并用AE的长度表示出正方形EFGH的面积是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
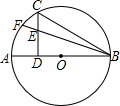 如图,已知AB是⊙O的直径,CD⊥AB于点D,E是CD上一点,BF交半圆于F.求证:BC2=BE•BF.
如图,已知AB是⊙O的直径,CD⊥AB于点D,E是CD上一点,BF交半圆于F.求证:BC2=BE•BF. 作出函数y=
作出函数y=