Question

1．如图，抛物线y=ax²+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．
（1）求抛物线的表达式；
（2）直按写出点C的坐标，并求出△ABC的面积；
（3）若点M在直线BH上运动，点．N在x轴上，且MN⊥CM，当以点C、M、N为顶点的三角形和△ABH相似时，请求出此时△CMN的面积．
（4）把抛物线沿直线AB平移，设平移后的抛物线与AB的交点为E，F（点E在F下方），当∠EHF=45°时，请直接写出点E的坐标．

Answer 1

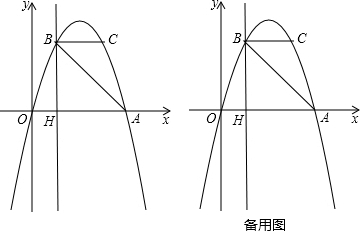
分析 （1）利用待定系数法求二次函数的表达式；
（2）根据二次函数的对称轴x=2写出点C的坐标为（3，3），根据面积公式求△ABC的面积；
（3）分别以点C、M、N为直角顶点分三类进行讨论，利用全等三角形和勾股定理求CM或CN的长，利用面积公式进行计算．
（4）分两种情形①当点E在BA的延长线上时，将△AHE绕点H逆时针旋转90°得到△HBE′，连接FE′，先证明AE²+BF²=EF²，由AB=EF=3$\sqrt{2}$，推出BF=AE=3，由此即可求出点E坐标．②当点E在AB的延长线上时，同理可得BE=3，即可解决问题．

解答 解：（1）把点A（4，0），B（1，3）代入抛物线y=ax²+bx中，
得   $\left\{\begin{array}{l}{16a+4b=0}\\{a+b=0}\end{array}\right.$解得：$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$，
∴抛物线表达式为：y=-x²+4x；

（2）点C的坐标为（3，3），
又∵点B的坐标为（1，3），
∴BC=2，
∴S_△ABC=$\frac{1}{2}$×2×3=3；                                

（3）以点C、M、N为顶点的三角形为等腰直角三角形时，分三类情况讨论：
①以点M为直角顶点且M在x轴上方时，如图2中，CM=MN，∠CMN=90°，
则△CBM≌△MHN，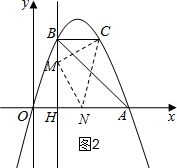

∴BC=MH=2，BM=HN=3-2=1，
∴M（1，2），N（2，0），
由勾股定理得：MC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∴S_△CMN=$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$=$\frac{5}{2}$；

②以点M为直角顶点且M在x轴下方时，如图3中，作辅助线，构建如图所示的两直角三角形：Rt△NEM和Rt△MDC，
得Rt△NEM≌Rt△MDC，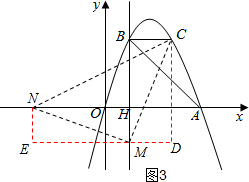

∴EM=CD=5，MD=ME=2，
由勾股定理得：CM=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$，
∴S_△CMN=$\frac{1}{2}$×$\sqrt{29}$×$\sqrt{29}$=$\frac{29}{2}$；

③以点N为直角顶点且N在y轴左侧时，如图4，CN=MN，∠MNC=90°，作辅助线，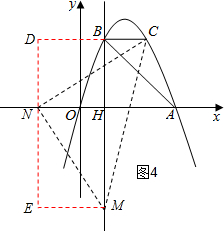

同理得：CN=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$，
∴S_△CMN=$\frac{1}{2}$×$\sqrt{34}$×$\sqrt{34}$=17；

④以点N为直角顶点且N在y轴右侧时，作辅助线，如图5，同理得：CN=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，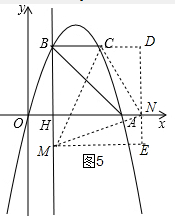

∴S_△CMN=$\frac{1}{2}$×$\sqrt{10}$×$\sqrt{10}$=5；
⑤以C为直角顶点时，不能构成满足条件的等腰直角三角形；
综上所述：△CMN的面积为：$\frac{5}{2}$或 $\frac{29}{2}$或17或5．

（4）如图6中，

①当点E在BA的延长线上时，将△AHE绕点H逆时针旋转90°得到△HBE′，连接FE′．
∵∠EHF=∠FHE′=45°，HF=HF，HE=HE′，
∴△HFE≌△HFE′，
∴EF=FE′，AE=BE′，
∵∠HBE′=∠HAE=135°，
∴∠E′BF=90°，
∴FE′²=BF²+BE′²，
∴AE²+BF²=EF²，
∵AB=EF=3$\sqrt{2}$，
∴BF=AE=3，
∴E（4+$\frac{3\sqrt{2}}{2}$，-$\frac{3\sqrt{2}}{2}$），
②当点E在AB的延长线上时，同理可得BE=3，E（1-$\frac{3\sqrt{2}}{2}$，3+$\frac{3\sqrt{2}}{2}$）．
综上所述，当∠EHF=45°时，点E的坐标为（4+$\frac{3\sqrt{2}}{2}$，-$\frac{3\sqrt{2}}{2}$）或（1-$\frac{3\sqrt{2}}{2}$，3+$\frac{3\sqrt{2}}{2}$）．

点评 本题是二次函数的综合题，考查了利用待定系数法求二次函数的表达式，考查了等腰直角三角形和全等三角形的判定和性质；本题的一般思路为：①根据函数的表达式设出点的坐标，利用面积公式直接表示或求和或求差列式，求出该点的坐标；②利用等腰直角三角形的两直角边相等，构建两直角三角形全等，再利用全等性质与点的坐标结合解决问题．