题目内容

13．通分：$\frac{a+2}{{a}^{2}-2a+1}$，$\frac{a+1}{{a}^{2}+a-2}$，$\frac{2a}{{a}^{2}+4a+4}$．

分析 先把分母因式分解，再找出最简公分母，最后根据分式的基本性质通分即可．

解答 解：$\frac{a+2}{{a}^{2}-2a+1}$=$\frac{a+2}{（a-1）^{2}}$=$\frac{（a+2）^{3}}{（a-1）^{2}（a+2）^{2}}$，
$\frac{a+1}{{a}^{2}+a-2}$=$\frac{a+1}{（a-1）（a+2）}$=$\frac{（{a}^{2}-1）（a+2）}{（a-1）^{2}（a+2）^{2}}$，
$\frac{2a}{{a}^{2}+4a+4}$=$\frac{2a}{（a+2）^{2}}$=$\frac{2a（a-1）^{2}}{（a-1）^{2}（a+2）^{2}}$．

点评 此题考查了通分，关键是把分母因式分解，找出最简公分母，用到的知识点是分式的基本性质．

练习册系列答案
相关题目
3．为纪念红军长征胜利80周年，特技飞行队在名胜风景旅游区--张家界天门洞特技表演，其中一架飞机起飞后的高度变化如表：
高度变化记作
上升4.5km+4.5km
下降3.2km-3.2km
上升1.1km+1.1km
下降1.4km-1.4km
（1）此时这架飞机比起飞点高了多少千米？
（2）如果飞机每上升或下降1千米需消耗2升燃油，那么这架飞机在这4个动作表演过程中，一共消耗了多少升燃油？
（3）如果飞机做特技表演时，有4个规定动作，起飞后高度变化如下：上升3.8千米，下降2.9千米，再上升1.6千米．若要使飞机最终比起飞点高出1千米，问第4个动作是上升还是下降，上升或下降多少千米？
4．计算下列各式：
（1）$\sqrt{（3.14-π）^{2}}$；
（2）-（-$\sqrt{{3}^{2}}$）2；
（3）$\sqrt{[（\frac{2}{3}）^{-1}]^{2}}$；
（4）（$\frac{3}{\sqrt{0．{5}^{2}}}$）2．
1．如图，抛物线y=ax2+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．
（1）求抛物线的表达式；
（2）直按写出点C的坐标，并求出△ABC的面积；
（3）若点M在直线BH上运动，点．N在x轴上，且MN⊥CM，当以点C、M、N为顶点的三角形和△ABH相似时，请求出此时△CMN的面积．
（4）把抛物线沿直线AB平移，设平移后的抛物线与AB的交点为E，F（点E在F下方），当∠EHF=45°时，请直接写出点E的坐标．
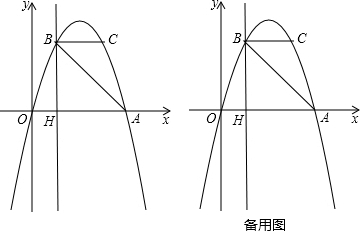
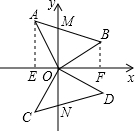8．如图，在直角坐标系中，等腰直角△OAB的顶点与原点重合，△OCD与△OAB关于x轴对称，点C的对称点是A，点D的对称点是B，AB交y轴于点M，CD交y轴于点N．
（1）作AE⊥x轴于E，作BF⊥x轴于F，若∠BOF=27°，求∠EAO与∠AMO的度数；
（2）若点D的坐标为（2，-1），请直接写出点B、A的坐标；
（3）在（2）的条件下，求MN的长．
18．等腰三角形腰上的高所在直线所夹的锐角为70°，则等腰三角形的顶角的度数为20°或160°．
5．出租车司机小王某天上午营运全是在东西走向的路上进行，如果规定向东为正，向西为负，他这天上午行车里程（单位：千米）如下：+8，+4，-1，-3，+6，-5，-2，-7，+4，+6，-9，-11．
（1）将第几名乘客送到目的地时，小王刚好回到上午出发点？
（2）将最后一名乘客送到目的地时，小王距上午出发点多远？
（3）若汽车耗油量为0.4升/千米，这天上午小王耗油多少升？
2．已知函数y=（m2+m）x${\;}^{{m}^{2}-m}$-2x是关于x的二次函数，求不等式（m-4）x＞m+2的解集．
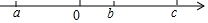18．有理数a、b、c在数轴上的位置如图：化简：|b-c|+2|a+b|-|c-a|

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网